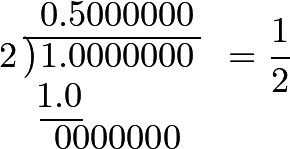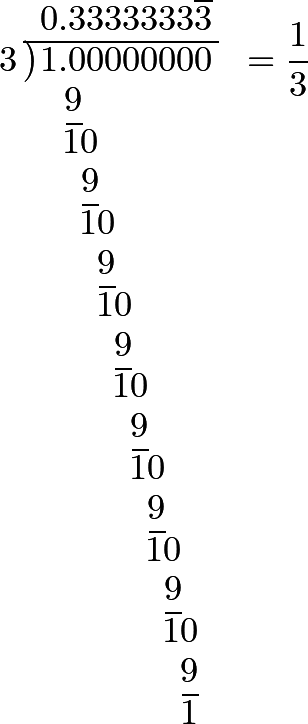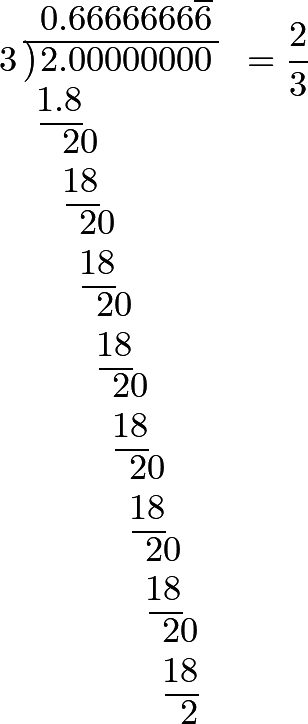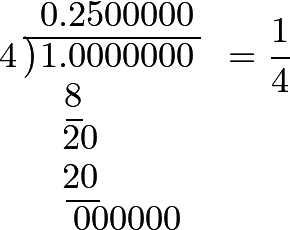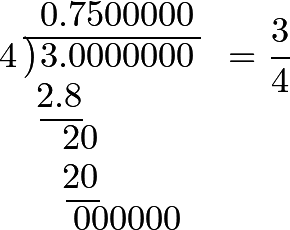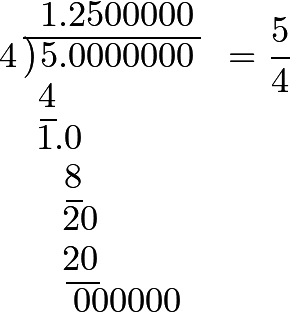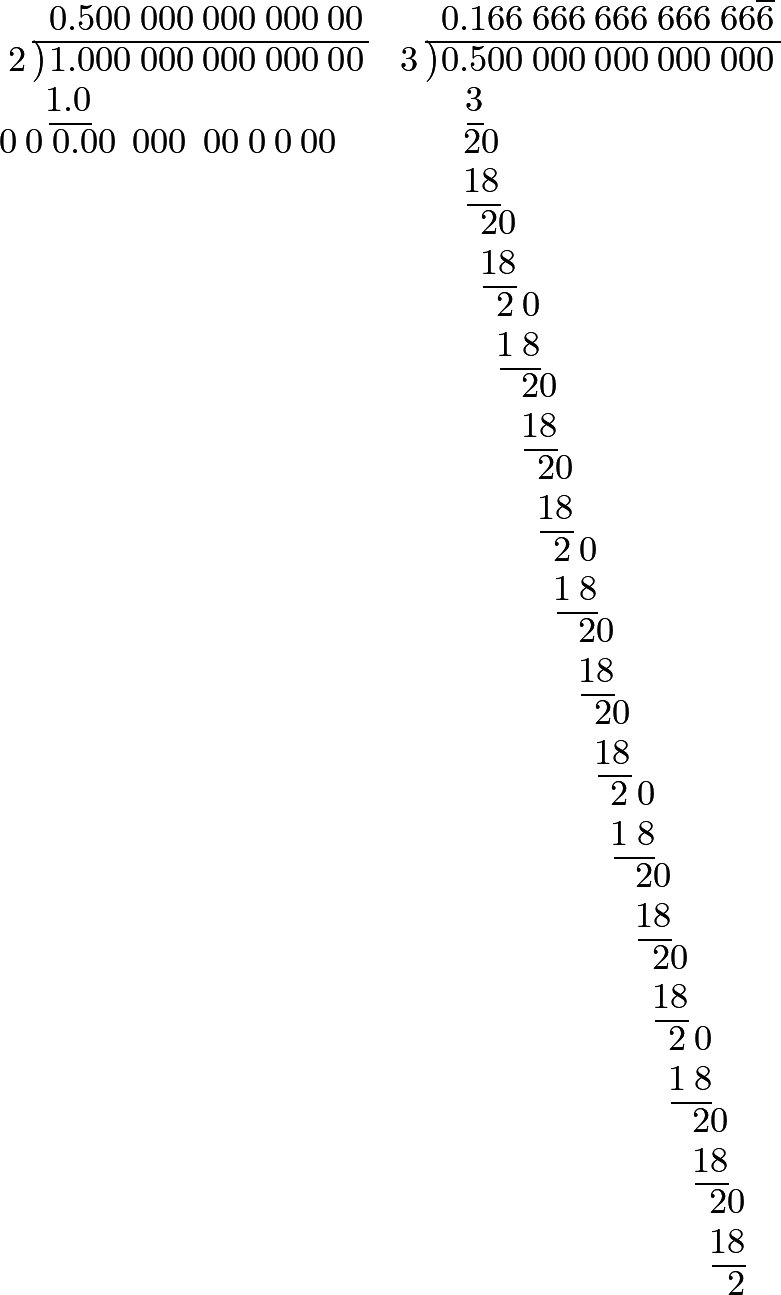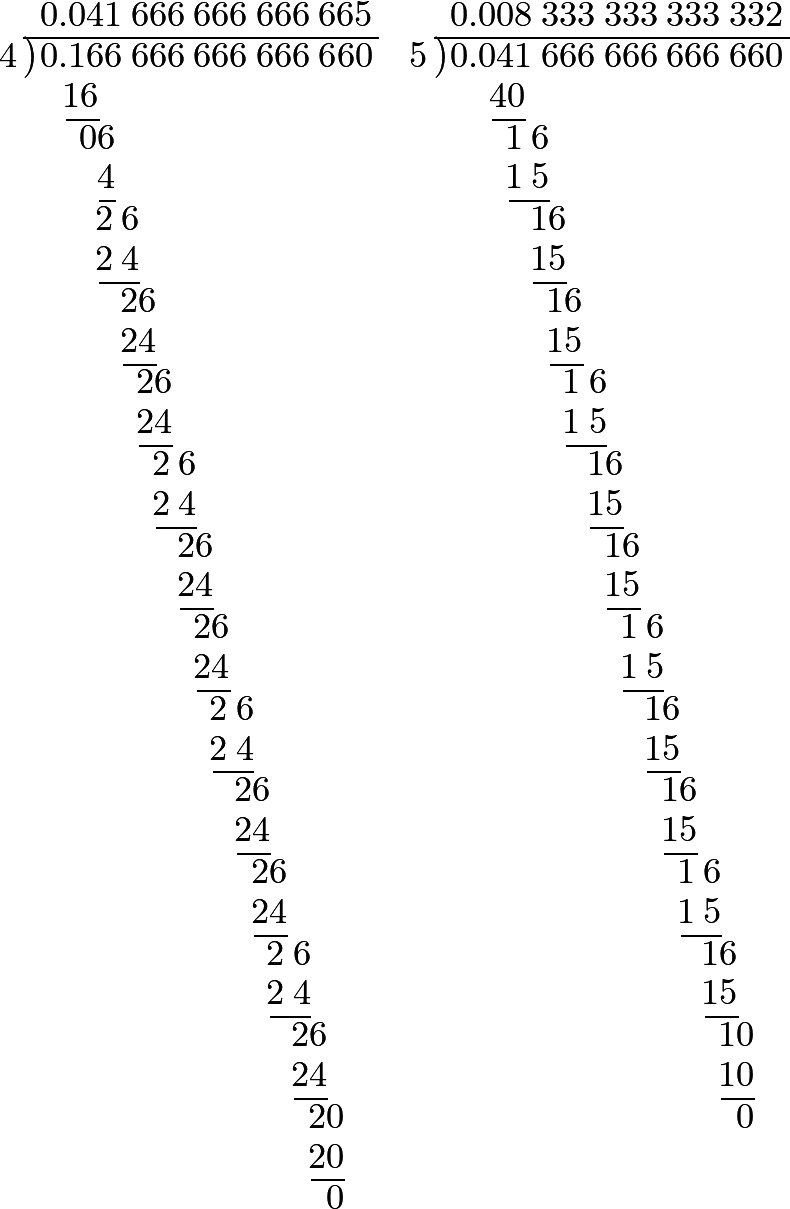Chapter 12. "Of Infinite Decimal Fractions."
Part I. Section III. Chapter 12. “Of Infinite Decimal Fractions.”
525 We have already seen, in logarithmic calculations, that Decimal Fractions are employed instead of Vulgar Fractions: the same are also advantageously employed in other calculations. It will therefore be very necessary to show how a vulgar fraction may be transformed into a decimal fraction; and, conversely, how we may express the value of a decimal, by a vulgar fraction.
526 Let it be required, in general, to change the fraction \(\frac{a}{b}\), into a decimal. As this fraction expresses the quotient of the division of the numerator \(a\) by the denominator \(b\), let us write, instead of \(a\), the quantity \(a.0000000\), whose value does not at all differ from that of \(a\), since it contains neither tenth parts, hundredth parts, nor any other parts whatever. If we now divide the quantity by the number \(b\), according to the common rules of division, observing to put the point in the proper place, which separates the decimal and the integers, we shall obtain the decimal sought. This is the whole of the operation, which we shall illustrate by some examples.
Let there be given first the fraction ½, and the division in decimals will assume this form:
Hence it appears, that ½ is equal to 0.5000000 or 0.5; which is sufficiently evident, since this decimal fraction represents ⁵⁄₁₀, which is equivalent to ½.
527 Let now ⅓ be the given fraction, and we shall have,
This shows, that the decimal fraction, whose value is ⅓, cannot, strictly, ever be discontinued, but that it goes on, to infinity, repeating always the number 3; which agrees with what has been already shown, Art. 523; namely, that the fractions
\[\frac{3}{10}+\frac{3}{100}+\frac{3}{1000}+\frac{3}{10000}+\textrm{etc., to infinity} = \frac{1}{3}.\]The decimal fraction which expresses the value of ⅔, is also continued to infinity; for we have,
Which is also evident from what we have just said, because ⅔ is the double of ⅓.
528 If ¼ be the fraction proposed, we have
So that ¼ is equal to 0.2500000, or to 0.25: which is evidently true, since
²⁄₁₀ + ⁵⁄₁₀₀ = ²⁰⁄₁₀₀ + ⁵⁄₁₀₀ = ²⁵⁄₁₀₀ = ¼.
In like manner, we should have for the fraction ¾,
So that ¾ = 0.75: and in fact
⁷⁄₁₀ + ⁵⁄₁₀₀ = ⁷⁰⁄₁₀₀ + ⁵⁄₁₀₀ = ⁷⁵⁄₁₀₀ = ¾.
The fraction ⁵⁄₄ is changed into a decimal fraction, by making
Now,
1 + ²⁵⁄₁₀₀ = 1 + ¼ = ⁵⁄₄.
529 In the same manner, ⅕ will be found equal to 0.2; ⅖ to 0.4; ⅗ to 0.6; ⅘ to 0.8; ⁵⁄₅ to 1; ⁶⁄₅ to 1.2, etc.
When the denominator is 6, we find ⅙ = 0.1666666,etc. which is equal to 0.666666 - 0.5: but 0.666666 = ⅔, and 0.5 = ½, wherefore 0.1666666 = ⅔ - ½; or ⁴⁄₆ - ³⁄₆ = ⅙.
We find, also, ²⁄₆ = 0.333333,etc. = ⅓; but ³⁄₆ becomes 0.5000000 = ½; also ⅚ = 0.833333 = 0.333333 + 0.5, that is to say, ⅓ + ½; or ²⁄₆ + ³⁄₆ = ⅚.
530 When the denominator is 7, the decimal fractions become more complicated. For example, we find
⅐ = 0.142857;
however it must be observed that these six figures are continually repeated. To be convinced, therefore, that this decimal fraction precisely expresses the value of ⅐, we may transform it into a geometrical progression, whose first term is ¹⁴²⁸⁵⁷⁄₁₀₀₀₀₀₀, the ratio being ¹⁄₁₀₀₀₀₀₀; and consequently, the sum equals
\[\dfrac{\dfrac{142857}{1000000}}{1-\dfrac{1}{1000000}}=\dfrac{142857}{1000000}=\dfrac{1}{7}.\]531 We may prove, in a manner still more easy, that the decimal fraction, which we have found, is exactly equal to ⅐; for, by substituting for its value the letter \(s\), we have
And, dividing by 999999, we have \(s\) = ¹⁴²⁸⁵⁷⁄₉₉₉₉₉₉ = ⅐. Wherefore the decimal fraction, which was represented by \(s\), is equal to ⅐.
532 In the same manner, ²⁄₇ may be transformed into a decimal fraction, which will be 0.28571428,etc. and this enables us to find more easily the value of the decimal fraction which we have represented by \(s\); because 0.28571428,etc. must be the double of it, and, consequently, equal to \(2s\). Now we have seen that
\[100s=14.28571428571,\textrm{etc.}\]So that subtracting
\[2s=0.28571428571,\textrm{etc.}\]there remains
\[98s=14\]wherefore \(s=\frac{14}{98}=\frac{1}{7}\).
We also find ³⁄₇ = 0.42857142857,etc. which, according to our supposition, must be equal to \(3s\); and we have found that
\[10s=1.42857142857,\textrm{etc.}\]So that subtracting
\[3s=0.42857142857,\textrm{etc.}\]we have \(7s=1\), wherefore \(s=\frac{1}{7}\).
533 When a proposed fraction, therefore, has the denominator 7, the decimal fraction is infinite, and 6 figures are continually repeated; the reason of which is easy to perceive, namely, that when we continue the division, a remainder must return, sooner or later, which we have had already. Now, in this division, 6 different numbers only can form the remainder, namely 1, 2, 3, 4, 5, 6; so that, at least, after the sixth division, the same figures must return; but when the denominator is such as to lead to a division without remainder, these cases do not happen.
534 Suppose now that 8 is the denominator of the fraction proposed: we shall laid the following decimal fractions:
⅛ = 0.125; ²⁄₈ = 0.25; ⅜ = 0.375; ⁴⁄₈ = 0.5; ⅝ = 0.625; ⁶⁄₈ = 0.75; ⅞ = 0.875, etc.
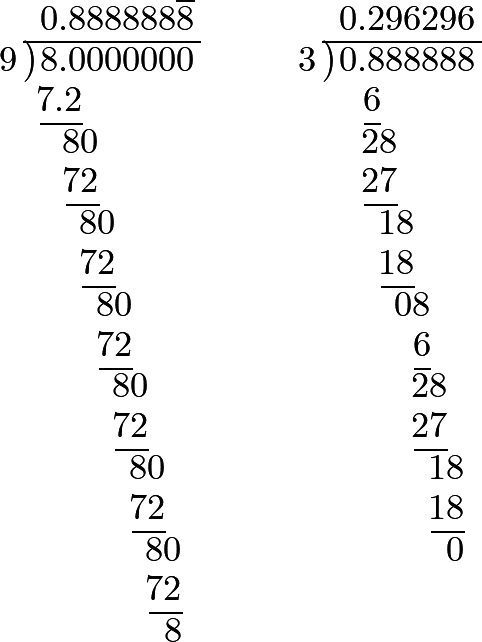
535 If the denominator be 9, we have
⅑ = 0.111,etc.; ²⁄₉ = 0.222,etc.; ³⁄₉ = 0.333,etc.
And if the denominator be 10, we have ⅒ = 0.1, ²⁄₁₀ = 0.2, ³⁄₁₀ = 0.3. This is evident from the nature of decimals, as also that ¹⁄₁₀₀ = 0.01; ³⁷⁄₁₀₀ = 0.37; ²⁵⁶⁄₁₀₀₀ = 0.256; ²⁴⁄₁₀₀₀₀ = 0.0024, etc.
536 If 11 be the denominator of the given fraction, we shall have ¹⁄₁₁ = 0.0909090,etc. Now, suppose it were required to find the value of this decimal fraction: let us call it \(s\), and we shall have
\[\begin{array}{rrr} s & = & 0.090909, \\ 10s & = & 0.909090, \\ 100s & = & 9.09090. \end{array}\]If, therefore, we subtract from the last the value of \(s\), we shall have \(99s=9\), and consequently \(s=\frac{9}{99}=\frac{1}{11}\); thus also,
²⁄₁₁ = 0.181818,etc.
³⁄₁₁ = 0.272727,etc.
⁶⁄₁₁ = 0.545454,etc.
537 There are a great number of decimal fractions, therefore, in which one, two, or more figures constantly recur, and which continue thus to infinity. Such fractions are curious, and we shall shew how their values may be easily found.
Let us first suppose, that a single figure is constantly repeated, and let us represent it by \(a\), so that \(s=0.aaaaaaa\). We have
\[10s=a.aaaaaaa\]and subtracting
\[s=0.aaaaaaa\]we have
\[9s=a;\]wherefore \(s=\dfrac{a}{9}\).
538 When two figures are repeated, as \(ab\), we have \(s=0.ababab\). Therefore \(100s=ab.ababab\); and if we subtract \(s\) from it, there remains \(99s=ab\): consequently, \(s=\dfrac{ab}{99}\).
When three figures, as \(abc\), are found repeated, we have \(s=0.abcabcabc\); consequently, \(1000s=abc.abcabc\); and subtracting \(s\) from it, there remains \(999s=abc\); wherefore, \(s=\dfrac{abc}{999}\), and so on.
Whenever, therefore, a decimal fraction of this kind occurs, it is easy to find its value. Let there be given, for example, 0.296296: its value will be ²⁹⁶⁄₉₉₉ = ⁸⁄₂₇, by dividing both its terms by 37.
This fraction ought to give again the decimal fraction proposed; and we may easily be convinced that this is the real result, by dividing 8 by 9, and then that quotient by 3, because 27 = 3 · 9: thus, we have
which is the decimal fraction that was proposed.
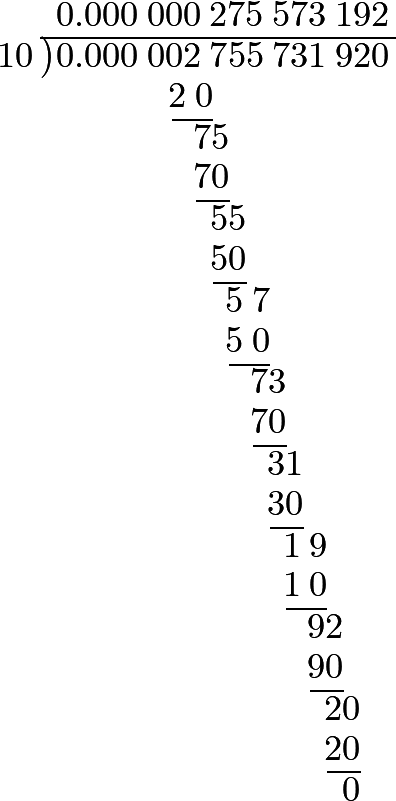
539 Suppose it were required to reduce the fraction
\[\dfrac{1}{1\cdot 2\cdot 3\cdot 4\cdot 5\cdot 6\cdot 7\cdot 8\cdot 9\cdot 10},\]to a decimal. The operation would be as follows:
Editions
- Leonhard Euler. Elements of Algebra. Translated by Rev. John Hewlett. Third Edition. Longmans, Hurst, Rees, Orme, and Co. London. 1822.
- Leonhard Euler. Vollständige Anleitung zur Algebra. Mit den Zusätzen von Joseph Louis Lagrange. Herausgegeben von Heinrich Weber. B. G. Teubner. Leipzig and Berlin. 1911. Leonhardi Euleri Opera omnia. Series prima. Opera mathematica. Volumen primum.