Mathematica plots

Bell, Jordan. “Estimates for the Norms of Products of Sines and Cosines.” Journal of Mathematical Analysis and Applications 405, no. 2 (2013): 530–45. https://doi.org/10.1016/j.jmaa.2013.04.010.

PDF

\[P_n(\theta) = \prod_{k=1}^n (1-e^{ik\theta})\] \[P_n(\theta)=(-2i)^n e^{\frac{iN\theta}{2}} \prod_{k=1}^n \sin\bigg(\frac{k\theta}{2} \bigg), \qquad N=\frac{n(n+1)}{2}\]
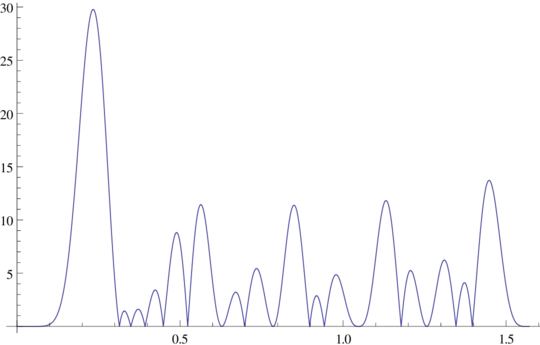
Plot of sine product for n=1 to 10
\(\prod_{k=1}^{10} 2|\sin(k \theta)|\) for \(0 \leq \theta \leq \frac{\pi}{2}\)
\[‖f‖_{L^1} = \frac{1}{2\pi} \int_0^{2\pi} |f(\theta)| d\theta\] \[K = \log 2 + \max_{0 < w < 1} \Bigg( \frac{1}{w} \int_0^w \log \sin(\pi t) dt \Bigg)\]
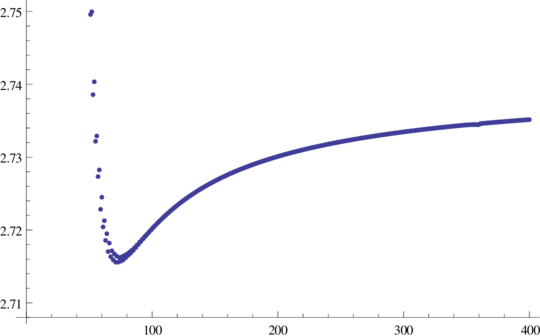
Plot of sine product L1 norms for n=1 to 400
\(\frac{‖P_n‖_{L^1}}{e^{nK} n^{-1}}\) for \(n=1,\ldots,400\)
\[‖f‖_{L^2} = \left(\frac{1}{2\pi} \int_0^{2\pi} |f(\theta)|^2 d\theta\right)^{\frac{1}{2}}\]
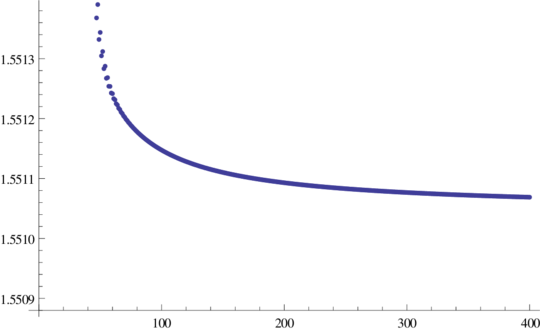
Plot of sine product L2 norms for n=1 to 400
\(\frac{‖P_n‖_{L^2}}{e^{nK}n^{-1/4}}\) for \(n=1,\ldots,400\)
\[Q_n(\theta) = \prod_{k=1}^n (1+e^{ik\theta})\] \[Q_n(\theta)=2^n e^{\frac{iN\theta}{2}} \prod_{k=1}^n \cos\big(\frac{k\theta}{2} \big), \quad N=\frac{n(n+1)}{2}\]
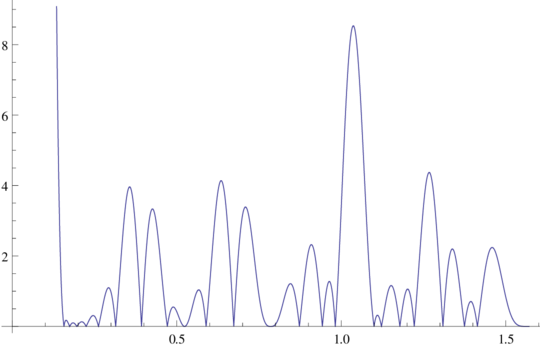
Plot of cosine product for n=1 to 10
\(\prod_{k=1}^{10} 2|\cos(k \theta)|\) for \(0 \leq \theta \leq \frac{\pi}{2}\)
\[\widehat{f}(k) = \int_0^{2\pi} f(\theta) e^{-ik\theta} d\theta,\quad k \in \mathbb{Z}\] \[‖\widehat{f}‖_{\ell^1} = \sum_{k \in \mathbb{Z}} |\widehat{f}(k)|\]
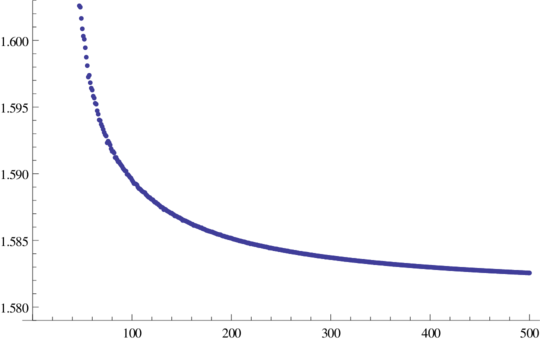
Plot of l1 norms of Fourier coefficients of Pn for n=1 to 500
\(\frac{‖\widehat{P}_n‖_{\ell^1}}{e^{Kn}n^{1/2}}\) for \(n=1,\ldots,500\)
\[‖\widehat{f}‖_{\ell^3} = \left( \sum_{k \in \mathbb{Z}} |\widehat{f}(k)|^3 \right)^{\frac{1}{3}}\]
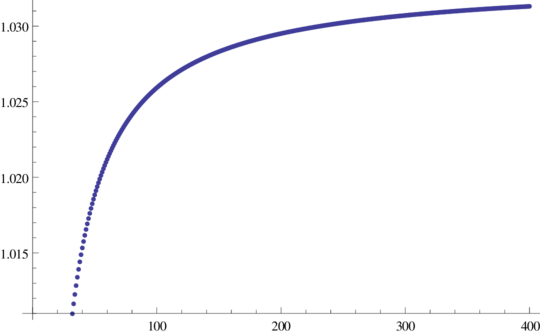
Plot of l3 norms of Fourier coefficients of Qn for n=1 to 400
\(\frac{‖\widehat{Q}_n‖_{\ell^3}}{2^n n^{-1}}\) for \(n=1,\ldots,400\)

Desmos plots

product of sin(kx)

product of cos(kx)