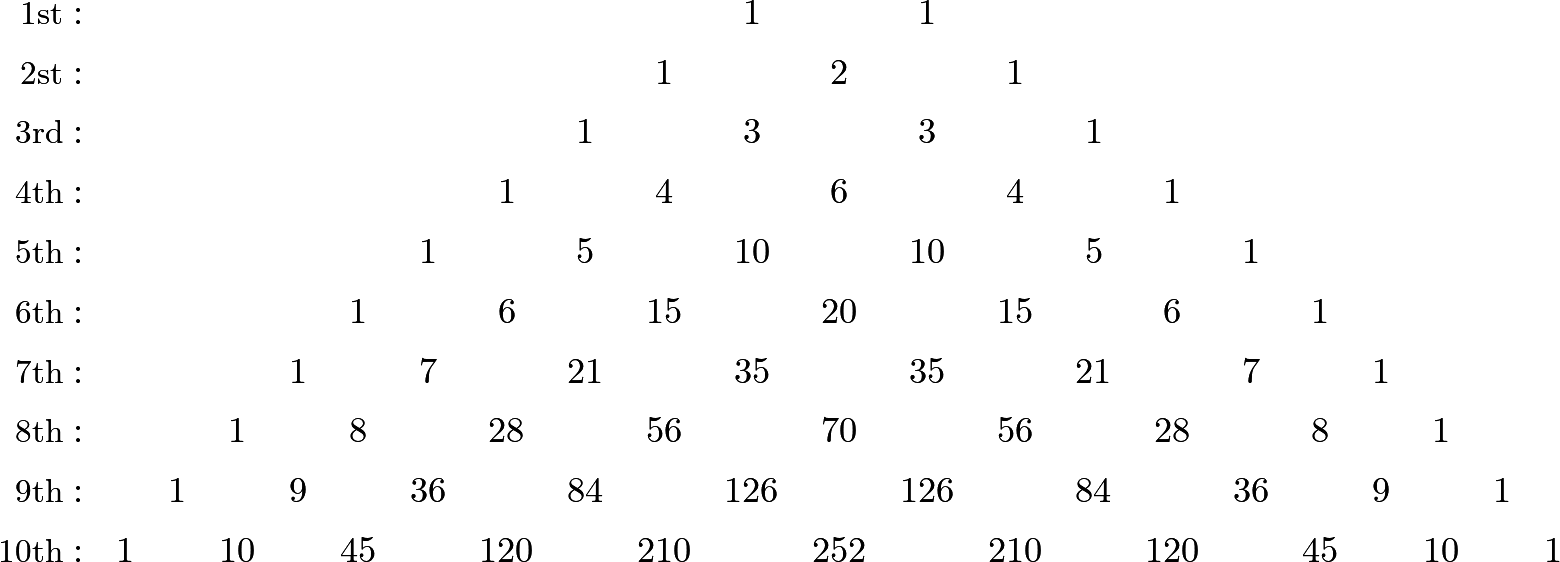Chapter 10. "Of the higher Powers of Compound Quantities."
Part I. Section II. Chapter 10. “Of the higher Powers of Compound Quantities.”
340 After squares and cubes, we must consider higher powers, or powers of a greater number of degrees; which are generally represented by exponents in the manner which we before explained: we have only to remember, when the root is compound, to enclose it in a parentheses: thus, \((a + b)^5\) means that \(a + b\) is raised to the fifth power, and \((a - b)^6\) represents the sixth power of \(a - b\), and so on. We shall in this chapter explain the nature of these powers.
341 Let \(a + b\) be the root, or the first power, and the higher powers will be found, by multiplication, in the following manner:
\[\begin{array}{rrrr} (a+b)^1=&a&+b&\\ &a&+b&\\ \hline &a^2&+ab&\\ &&+ab&+b^2\\ \hline (a+b)^2=&a^2&+2ab&+b^2 \end{array}\]\[\begin{array}{rrrrr} (a+b)^2=&a^2&+2ab&+b^2&\\ &a&+b&&\\ \hline &a^3&+2a^2b&+ab^2&\\ &&+a^2b&+2ab^2&+b^3\\ \hline (a+b)^3=&a^3&+3a^2b&+3ab^2&+b^3 \end{array}\]
\[\begin{array}{rrrrrr} (a+b)^3=&a^3&+3a^2b&+3ab^2&+b^3\\ &a&+b&&&\\ \hline &a^4&+3a^3b&+3a^2b^2&+ab^3&\\ &&+a^3b&+3a^2b^2&+3ab^3&+b^4\\ \hline (a+b)^4=&a^4&+4a^3b&+6a^2b^2&+4ab^3&+b^4 \end{array}\]
\[\begin{array}{rrrrrrr} (a+b)^4=&a^4&+4a^3b&+6a^2b^2&+4ab^3&+b^4&\\ &a&+b&&&&\\ \hline &a^5&+4a^4b&+6a^3b^2&+4a^2b^3&+ab^4&\\ &&+a^4b&+4a^3b^2&+6a^2b^3&+4ab^4&+b^5\\ \hline (a+b)^5=&a^5&+5a^4b&+10a^3b^2&+10a^2b^3&+5ab^4&+b^5 \end{array}\]
\[\begin{array}{rrrrrrrr} (a+b)^5=&a^5&+5a^4b&+10a^3b^2&+10a^2b^3&+5ab^4&+b^5&\\ &a&+b&&&&&\\ \hline &a^6&+5a^5b&+10a^4b^2&+10a^3b^3&+5a^2b^4&+ab^5&\\ &&+a^5b&+5a^4b^2&+10a^3b^3&+10a^2b^4&+5ab^5&+b^6\\ \hline (a+b)^6=&a^6&+6a^5b&+15a^4b^2&+20a^3b^3&+15a^2b^4&+6ab^5&+b^6 \end{array}\]
etc.
342 The powers of the root \(a - b\) are found in the same manner; and we shall immediately perceive that they do not differ from the preceding, excepting that the 2nd, 4th, 6th, etc. terms are affected by the sign minus.
\[\begin{array}{rrrr} (a-b)^1=&a&-b&\\ &a&-b&\\ \hline &a^2&-ab&\\ &&-ab&+b^2\\ \hline (a-b)^2=&a^2&-2ab&+b^2 \end{array}\]\[\begin{array}{rrrrr} (a-b)^2=&a^2&-2ab&+b^2&\\ &a&-b&&\\ \hline &a^3&-2a^2b&+ab^2&\\ &&-a^2b&+2ab^2&-b^3\\ \hline (a-b)^3=&a^3&-3a^2b&+3ab^2&+b^3 \end{array}\]
\[\begin{array}{rrrrrr} (a-b)^3=&a^3&-3a^2b&+3ab^2&-b^3\\ &a&-b&&&\\ \hline &a^4&-3a^3b&+3a^2b^2&-ab^3&\\ &&-a^3b&+3a^2b^2&-3ab^3&+b^4\\ \hline (a-b)^4=&a^4&-4a^3b&+6a^2b^2&-4ab^3&+b^4 \end{array}\]
\[\begin{array}{rrrrrrr} (a-b)^4=&a^4&-4a^3b&+6a^2b^2&-4ab^3&+b^4&\\ &a&-b&&&&\\ \hline &a^5&-4a^4b&+6a^3b^2&-4a^2b^3&+ab^4&\\ &&-a^4b&+4a^3b^2&-6a^2b^3&+4ab^4&-b^5\\ \hline (a-b)^5=&a^5&-5a^4b&+10a^3b^2&-10a^2b^3&+5ab^4&-b^5 \end{array}\]
\[\begin{array}{rrrrrrrr} (a-b)^5=&a^5&-5a^4b&+10a^3b^2&-10a^2b^3&+5ab^4&-b^5&\\ &a&-b&&&&&\\ \hline &a^6&-5a^5b&+10a^4b^2&-10a^3b^3&+5a^2b^4&-ab^5&\\ &&-a^5b&+5a^4b^2&-10a^3b^3&+10a^2b^4&-5ab^5&+b^6\\ \hline (a-b)^6=&a^6&-6a^5b&+15a^4b^2&-20a^3b^3&+15a^2b^4&-6ab^5&+b^6 \end{array}\]
etc.
Here we see that all the odd powers of b have the sign -, while the even powers retain the sign +. The reason of this is evident; for since \(-b\) is a term of the root, the powers of tliat letter will ascend in the following series, \(-b\), \(+b^2\), \(-b^3\), \(+b^4\), \(-b^5\), \(+b^6\), etc. which clearly shows that the even powers must be affected by the sign +, and the odd ones by the contrary sign -.
343 An important question occurs in this place ; namely, how we may find, without being obliged to perform the same calculation, all the powers either of \(a+b\) or \(a-b\).
We must remark, in the first place, that if we can assign all the powers of \(a + b\), those of \(a - b\) are also found; since we have only to change the signs of the even terms, that is to say, of the second, the fourth, the sixth, etc.. The business then is to establish a rule, by which any power of \(a+b\), however high, may be determined without the necessity of calculating all the preceding powers.
344 Now, if from the powers which we have already determined we take away the numbers that precede each term, which are called the coefficients, we observe in all the terms a singular order: first, we see the first term \(a\) of the root raised to the power which is required; in the following terms, the powers of \(a\) diminish continually by unity, and the powers of \(b\) increase in the same proportion; so that the sum of the exponents of \(a\) and of \(b\) is always the same, and always equal to the exponent of the power required; and, lastly, we find the term \(b\) by itself raised to the same power. If therefore the tenth power of \(a + b\) were required, we are certain that the terms, without their coefficients, would succeed each other in the following order;
\[a^{10}, a^9 b, a^8b^2, a^7b^3, a^6b^4, a^5b^5, a^4b^6, a^3b^7, a^2b^8, ab^9, b^{10}.\]345 It remains therefore to shew how we are to determine the coefficients, which belong to those terms, or the numbers by which they are to be multiplied. Now, with respect to the first term, its coefficient is always unity; and, as to the second, its coefficient is constantly the exponent of the power. With regard to the other terms, it is not so easy to observe any order in their coefficients; but, if we continue those coefficients, we shall not fail to discover the law by which they are formed; as will appear from the following Table.
We see then that the tenth power of \(a+b\) will be
\[a^{10}+10a^9b+45a^8b^2+120a^7b^3+210a^6b^4+252a^5b^5+210a^4b^6+120a^3b^7+ 45a^2b^8+10ab^9+b^{10}.\]346 Now, with regard to the coefficients, it must be observed, that for each power their sum must be equal to the number 2 raised to the same power; for let \(a = 1\) and \(b = 1\), then each term, without the coefficients, will be 1; consequently, the value of the power will be simply the sum of the coefficients. This sum, in the preceding example, is 1024, and accordingly \((1+1)^{10}=2^{10}=1024\). It is the same with respect to all other powers; thus, we have for the
\[\begin{array}{rl} \textrm{1st}&1+1=2=2^1,\\ \textrm{2nd}&1+2+1=4=2^2,\\ \textrm{3rd}&=1+3+3+1=8=2^3,\\ \textrm{4th}&=1+4+6+4+1=16=2^4,\\ \textrm{5th}&=1+5+10+10+5+1=32=2^5,\\ \textrm{6th}&=1+6+15+20+15+6+1=64=2^6,\\ \textrm{7th}&=1+7+21+35+35+21+7+1=128=2^7,\\ &\textrm{etc.} \end{array}\]347 Another necessary remark, with regard to the coefficients, is, that they increase from the beginning to the middle, and then decrease in the same order. In the even powers, the greatest coefficient is exactly in the middle; but in the odd powers, two coefficients, equal and greater than the others, are found in the middle, belonging to the mean terms.
The order of the coefficients likewise deserves particular attention; for it is in this order that we discover the means of determining them for any power whatever, without calculating all the preceding powers. We shall here explain this method, reserving the demonstration however for the next chapter.
348 In order to find the coefficients of any power proposed, the seventh for example, let us write the following fractions one after the other:
\[\frac{7}{1},\frac{6}{2},\frac{5}{3},\frac{4}{4},\frac{3}{5},\frac{2}{6},\frac{1}{7}.\]In this arrangement, we perceive that the numerators begin by the exponent of the power required, and that they diminish successively by unity; while the denominators follow in the natural order of the numbers, 1, 2, 3, 4, etc. Now, the first coefficient being always 1, the first fraction gives the second coefficient; the product of the first two fractions, multiplied together, represents the third coefficient; the product of the three first fractions represents the fourth coefficient, and so on. Thus, the
\[\begin{array}{lll} \textrm{1st coefficient}&1&=1\\ \textrm{2nd coefficient}&\dfrac{7}{1}&=7\\ \textrm{3rd coefficient}&\dfrac{7 \cdot 6}{1\cdot 2}&=21\\ \textrm{4th coefficient}&\dfrac{7 \cdot 6 \cdot 5}{1\cdot 2 \cdot 3}&=35\\ \textrm{5th coefficient}&\dfrac{7 \cdot 6 \cdot 5 \cdot 4}{1\cdot 2 \cdot 3 \cdot 4}&=35\\ \textrm{6th coefficient}&\dfrac{7 \cdot 6 \cdot 5 \cdot 4 \cdot 3}{1\cdot 2 \cdot 3 \cdot 4 \cdot 5}&=21\\ \textrm{7th coefficient}&\dfrac{7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2}{1\cdot 2 \cdot 3 \cdot 4 \cdot 5 \cdot 6}&=7\\ \textrm{8th coefficient}&\dfrac{7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}{1\cdot 2 \cdot 3 \cdot 4 \cdot 5 \cdot 6 \cdot 7}&=1. \end{array}\]349 So that we have, for the second power, the fractions \(\frac{2}{1},\frac{1}{2}\); whence the first coefficient is 1, the second \(\frac{2}{1}=2\), and the third \(2 \cdot \frac{1}{2}=1\).
The third power furnishes the fractions \(\frac{3}{1},\frac{2}{2},\frac{1}{3}\); wherefore the
\[\begin{array}{lll} \textrm{1st coefficient}&&=1;\\ \textrm{2nd coefficient}&\dfrac{3}{1}&=3;\\ \textrm{3rd coefficient}&3 \cdot \dfrac{2}{2}&=3;\\ \textrm{4th coefficient}&\dfrac{3}{1} \cdot \dfrac{2}{2} \cdot \dfrac{1}{3}&=1.\\ \end{array}\]We have, for the fourth power, the fractions \(\frac{4}{1},\frac{3}{2},\frac{2}{3},\frac{1}{4}\), consequently, the
\[\begin{array}{lll} \textrm{1st coefficient}&&=1;\\ \textrm{2nd coefficient}&\dfrac{4}{1}&=4;\\ \textrm{3rd coefficient}&\dfrac{4}{1} \cdot \dfrac{3}{2}&=6;\\ \textrm{4th coefficient}&\dfrac{4}{1} \cdot \dfrac{3}{2} \cdot \dfrac{2}{3}&=4;\\ \textrm{5th coefficient}&\dfrac{4}{1} \cdot \dfrac{3}{2} \cdot \dfrac{2}{3} \cdot \dfrac{1}{4}&=1. \end{array}\]350 This rule evidently renders it unnecessary to find the coefficients of the preceding powers, as it enables us to discover immediately the coefficients which belong to any one proposed. Thus, for the tenth power, we write the fractions
\[\frac{10}{1},\frac{9}{2},\frac{8}{3},\frac{7}{4},\frac{6}{5},\frac{5}{6},\frac{4}{7},\frac{3}{8},\frac{2}{9},\frac{1}{10},\]by means of which we find the
\[\begin{array}{lll} \textrm{1st coefficient}&&=1;\\ \textrm{2nd coefficient}&\dfrac{10}{1}&=10;\\ \textrm{3rd coefficient}&10 \cdot \dfrac{9}{2}&=45;\\ \textrm{4th coefficient}&45 \cdot \dfrac{8}{3}&=120;\\ \textrm{5th coefficient}&120 \cdot \dfrac{7}{4}&=210;\\ \textrm{6th coefficient}&210 \cdot \dfrac{6}{5}&=252;\\ \textrm{7th coefficient}&252 \cdot \dfrac{5}{6}&=210;\\ \textrm{8th coefficient}&210 \cdot \dfrac{4}{7}&=120;\\ \textrm{9th coefficient}&120 \cdot \dfrac{3}{8}&=45;\\ \textrm{10th coefficient}&45 \cdot \dfrac{2}{9}&=10;\\ \textrm{11th coefficient}&10 \cdot \dfrac{1}{10}&=1. \end{array}\]351 We may also write these fractions as they are, without computing their value; and in this manner it is easy to express any power of \(a+b\). Thus,
\[(a+b)^{100}=a^{100}+\frac{100}{1}a^{99}b+\frac{100\cdot 99}{1\cdot 2}a^{98}b^2 +\frac{100\cdot 99\cdot 98}{1\cdot 2\cdot 3}a^{97}b^3 +\frac{100\cdot 99\cdot 98 \cdot 97}{1\cdot 2\cdot 3 \cdot 4}a^{96}b^4 +\textrm{etc.}\]Whence the law of the succeeding terms may be easily deduced.
Editions
- Leonhard Euler. Elements of Algebra. Translated by Rev. John Hewlett. Third Edition. Longmans, Hurst, Rees, Orme, and Co. London. 1822.
- Leonhard Euler. Vollständige Anleitung zur Algebra. Mit den Zusätzen von Joseph Louis Lagrange. Herausgegeben von Heinrich Weber. B. G. Teubner. Leipzig and Berlin. 1911. Leonhardi Euleri Opera omnia. Series prima. Opera mathematica. Volumen primum.