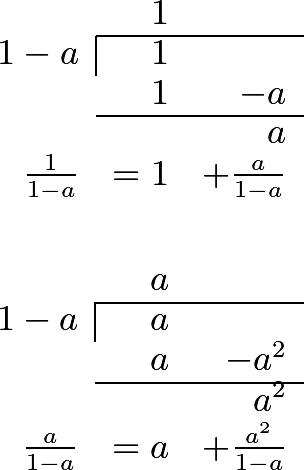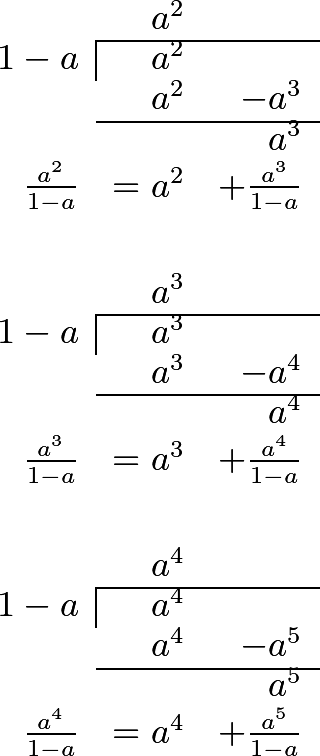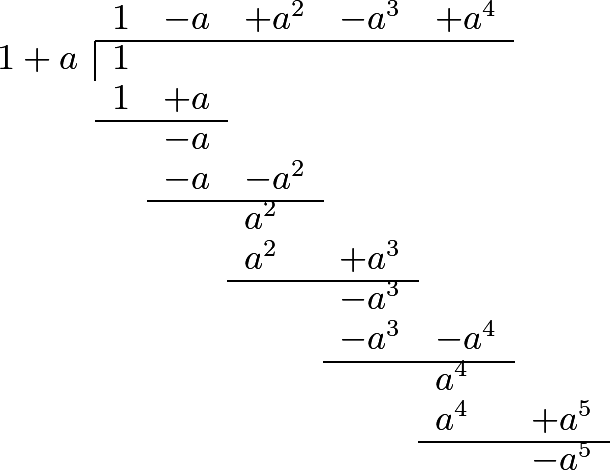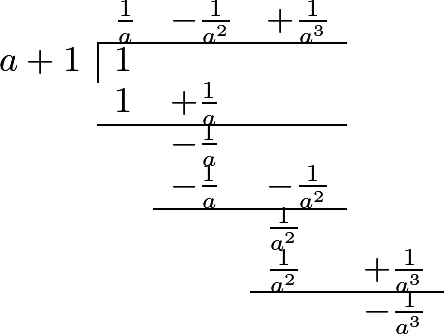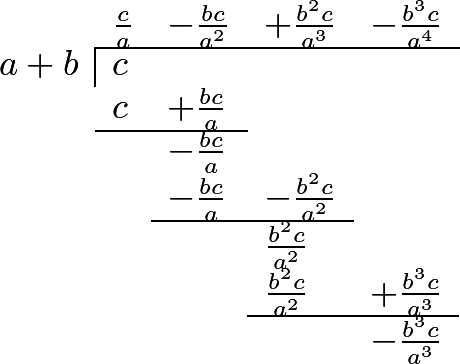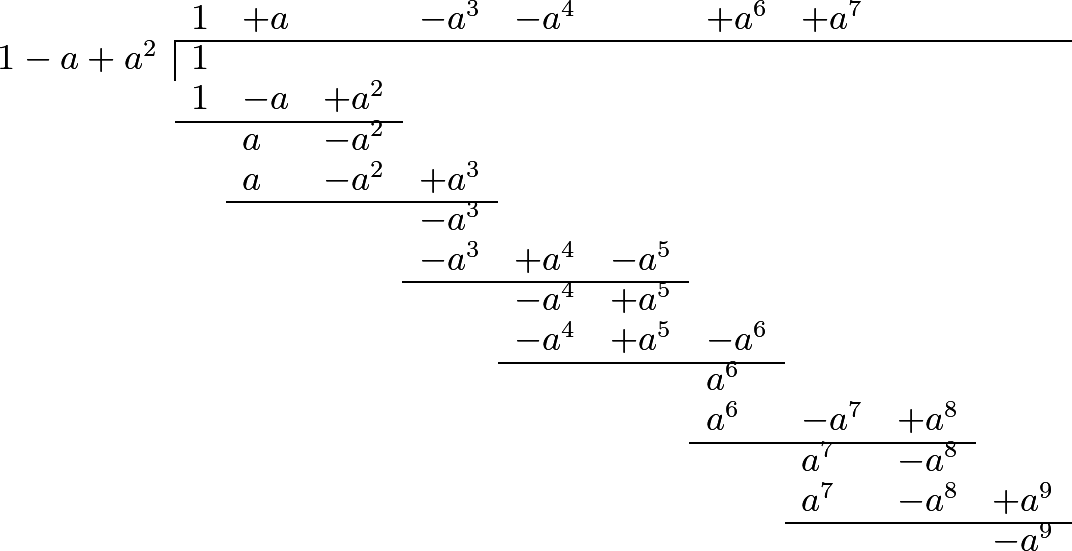Chapter 5. "Of the Resolution of Fractions into Infinite Series."
Part I. Section II. Chapter 5. “Of the Resolution of Fractions into Infinite Series.”
289 When the dividend is not divisible by the divisor, the quotient is expressed, as we have already observed, by a fraction: thus, if we have to divide 1 by \(1-a\), we obtain the fraction \(\dfrac{1}{1-a}\). This, however, does not prevent us from attempting the division according to the rules that have been given, nor from continuing it as far as we please; and we shall not fail thus to find the true quotient, though under different forms.
290 To prove this, let us actually divide the dividend 1 by the divisor \(1-a\), thus
291 This shows that the fraction \(\dfrac{1}{1-a}\) may be exhibited under all the following forms:
- \(1+\dfrac{a}{1-a}\),
- \(1+a+\dfrac{a^2}{1-a}\),
- \(1+a+a^2+\dfrac{a^3}{1-a}\),
- \(1+a+a^2+a^3+\dfrac{a^4}{1-a}\),
- \(1+a+a^2+a^3+a^4+\dfrac{a^5}{1-a}\), etc.
Now, by considering the first of these expressions, which is \(1+\dfrac{a}{1-a}\), and remembering that 1 is the same as \(\dfrac{1-a}{1-a}\), we have
\[1+\dfrac{a}{1-a}=\dfrac{1-a}{1-a}+\dfrac{a}{1-a} = \dfrac{1-a+a}{1-a} = \dfrac{1}{1-a}.\]If we follow the same process, with regard to the second expression, \(1+a+\dfrac{a^2}{1-a}\), that is to say, if we reduce the integral part \(1+a\) to the same denominator, \(1-a\), we shall have \(\dfrac{1-a^2}{1-a}\), to which if we add \(+\dfrac{a^2}{1-a}\), we shall have \(\dfrac{1-a^2+a^2}{1-a}\), that is to say, \(\dfrac{1}{1-a}\).
In the third expression, \(1+a+a^2+\dfrac{a^3}{1-a}\), the integers reduced to the denominator \(1-a\) make \(\dfrac{1-a^3}{1-a}\); and if we add to that the fraction \(\dfrac{a^3}{1-a}\), we have \(\dfrac{1}{1-a}\), as before; therefore all these expressions are equal in value to \(\dfrac{1}{1-a}\), the proposed fraction.
292 This being the case, we may continue the series as far as we please, without being under the necessity of performing any more calculations; and thus we shall have
\[\dfrac{1}{1-a}=1+a+a^2+a^3+a^4+a^5+a^6+a^7+\dfrac{a^8}{1-a};\]or we might continue this farther, and still go on without end; for which reason it may be said that the proposed fraction has been resolved into an infinite series, which is,
\[1+a+a^2+a^3+a^4+a^5+a^6+a^7+a^8+a^9+a^{10}+a^{11}+a^{12}+\textrm{etc.}\]to infinity: and there are sufficient grounds to maintain, that the value of this infinite series is the same as that of the fraction \(\dfrac{1}{1-a}\).
293 What we have said may at first appear strange; but the consideration of some particular cases will make it easily understood. Let us suppose, in the first place, \(a=1\); our series will become
1+1+1+1+1+1+1+etc.;
and the fraction \(\dfrac{1}{1-a}\), to which it must be equal, becomes \(\frac{1}{0}\). Now, we have before remarked, that \(\frac{1}{0}\) is a number infinitely great; which is therefore here confirmed in a satisfactory manner. See Art. 83 and 84.
Again, if we suppose \(a=2\), our series becomes
1 + 2 + 4 + 8 + 16 + 32 + 64 + etc. to infinity,
and its value must be the same as \(\dfrac{1}{1-2}\), that is to say, \(\dfrac{1}{-1}=-1\); which at first sight will appear absurd. But it must be remarked, that if we wish to stop at any term of the above series, we cannot do so without annexing to it the fraction which remains. Suppose, for example, we were to stop at 64, after having written
1 + 2 + 4 + 8 + 16 + 32 + 64,
we must add the fraction \(\frac{128}{1-2}\), or \(\dfrac{128}{-1}\), or -128; we shall therefore have 127 - 128, that is in fact -1.
Were we to continue the series without intermission, the fraction would be no longer considered; but, in that case, the series would still go on.
294 These are the considerations which are necessary, when we assume for a numbers greater than unity; but if we suppose a less than 1, the whole becomes more intelligible : for example, let \(a=\frac{1}{2}\); and we shall then have \(\dfrac{1}{1-a}=\dfrac{1}{1-\frac{1}{2}}=\dfrac{1}{\frac{1}{2}}=2\), which will be equal to the following series
1 + ½ + ¼ + ⅛ + ¹⁄₁₆ + ¹⁄₃₂ + ¹⁄₆₄ + ¹⁄₁₂₈ + etc.,
to infinity. Now, if we take only two terms of this series, we shall have 1 + ½, and it wants ½ of being equal to \(\dfrac{1}{1-a}=2\). If we take three terms, it wants ¼; for the sum is 1¾. If we take four terms, we have 1⅞, and the deficiency is only ⅛. Therefore, the more terms we take, the less the diiference becomes; and, consequently, if we continue the series to infinity, there will be no difference at all between its sum and the value of the fraction \(\dfrac{1}{1-a}\), or 2.
295 Let \(a=\frac{1}{3}\); and our fraction \(\dfrac{1}{1-a}\) will then be \(=\dfrac{1}{1-\frac{1}{3}}=\frac{3}{2}=1\frac{1}{2}\), which, reduced to an infinite series, becomes
1 + ⅓ + ⅑ + ¹⁄₂₇ + ¹⁄₈₁ + ¹⁄₂₄₃ + etc.,
which is consequently equal to \(\dfrac{1}{1-a}\).
Here, if we take two terms, we have 1⅓, and there wants ⅙. If we take three terms, we have 1⁴⁄₉, and there will still be wanting ¹⁄₁₈. If we take four terms, we shall have 1¹³⁄₂₇, and the difference will be ¹⁄₅₄; since, therefore, the error always becomes three times less, it must evidently vanish at last.
296 Suppose \(a=\frac{2}{3}\); we shall have \(\dfrac{1}{1-a}=\dfrac{1}{1-\frac{2}{3}}=3\),
= 1 + ⅔ + ⁴⁄₉ + ⁸⁄₂₇ + ¹⁶⁄₈₁ + ³²⁄₂₄₃ + etc.,
to infinity; and here, by taking first 1⅔, the error is 1⅓; taking three terms, which make 2⅑, the error is ⁸⁄₉; taking four terms, we have 2¹¹⁄₂₇, and the error is ¹⁶⁄₂₇.
297 If \(a=\frac{1}{4}\), the fraction is \(\dfrac{1}{1-\frac{1}{4}}=\dfrac{1}{\frac{3}{4}}=1\frac{1}{3}\); and the series becomes
1 + ¼ + ¹⁄₁₆ + ¹⁄₆₄ + ¹⁄₂₅₆ + etc.
The first two terms are equal to 1¼, which gives ¹⁄₁₂ for the error; and taking one term more, we have 1¹⁄₁₅, that is to say, only an error of ¹⁄₄₈.
298 In the same manner we may resolve the fraction \(\dfrac{1}{1+a}\), into an infinite series by actually dividing the numerator 1 by the denominator \(1+a\), as follows.
\[\dfrac{1}{1+a}=1-a+a^2-a^3+a^4+\dfrac{-a^5}{1-a}\]Whence it follows, that the fraction \(\dfrac{1}{1+a}\) is equal to the series,
\[1-a+a^2-a^3+a^4-a^5+a^6-a^7, \textrm{etc.}\]299 If we make \(a=1\), we have this remarkable comparison:
\[\dfrac{1}{1+a}=\frac{1}{2}=1-1+1-1+1-1+1-1, \textrm{etc.}\]to infinity; which appears rather contradictory; for if we stop at -1, the series gives 0; and if we finish at +1, it gives 1; but this is precisely what solves the difficulty; for since we must go on to infinity, without stopping either at -1 or +1, it is evident, that the sum can neither be 0 nor 1, but that this result must lie between these two, and therefore be ½.
300 Let us now make \(a=\frac{1}{2}\), and our fraction will be \(\dfrac{1}{1+\frac{1}{2}}=\frac{2}{3}\), which must therefore express the value of the series
1 - ½ + ¼ - ⅛ + ¹⁄₁₆ - ¹⁄₃₂ + ¹⁄₆₄, etc., to infinity; here if we take only the two leading terms of this series, we have ½, which is too small by ⅙; if we take three terms, we have ¾, which is too much by ¹⁄₁₂; if we take four terms, we have ⅝, which is too small by ¹⁄₂₄, etc.
301 Suppose again \(a=\frac{1}{3}\), our fraction will then be \(=\dfrac{1}{1+\frac{1}{3}}=\frac{3}{4}\), which must be equal to this series
1 - ⅓ + ⅑ - ¹⁄₂₇ + ¹⁄₈₁ - ¹⁄₂₄₃ + ¹⁄₇₂₉, etc., continued to infinity.
Now, by considering only two terms, we have ⅔, which is too small by ¹⁄₁₂; three terms make ⁷⁄₉, which is too much by ¹⁄₃₆; four terms give ²⁰⁄₂₇, which is too small by ¹⁄₁₀₈, and so on.
302 The fraction \(\dfrac{1}{1+a}\) may also be resolved into an infinite series another way; namely, by dividing 1 by \(a+1\), as follows:
\[\dfrac{1}{a+1} = \frac{1}{a} - \frac{1}{a^2} + \frac{1}{a^3} + \dfrac{-\frac{1}{a^3}}{a+1}\]Consequently, our fraction \(\dfrac{1}{1+a}\), is equal to the infinite series
\[\dfrac{1}{a+1} = \frac{1}{a} + \frac{1}{a^2} + \frac{1}{a^3} -\frac{1}{a^4} + \frac{1}{a^5} - \frac{1}{a^6}, \textrm{etc.}\]Let us make \(a=1\), and we shall have the series
1 - 1 + 1 - 1 + 1 - 1, etc. = ½,
as before: and if we suppose \(a=2\), we shall have the series
½ - ¼ + ⅛ - ¹⁄₁₆ + ¹⁄₃₂ - ¹⁄₆₄, etc. = ⅓.
303 In the same manner, by resolving the general fraction \(\dfrac{c}{a+b}\) into an infinite series, we shall have,
\[\dfrac{c}{a+b} = \frac{c}{a} - \frac{bc}{a^2} + \frac{bc^2}{a^3} - \frac{bc^3}{a^4} + \dfrac{-\frac{b^3c}{a^3}}{a+b}\]Whence it appears, that we may compare \(\dfrac{c}{a+b}\) with the series \(\frac{c}{a} - \frac{bc}{a^2} + \frac{bc^2}{a^3} - \frac{bc^3}{a^4}\), etc. continued to infinity.
Let \(a=2\), \(b=4\), and \(c=3\), and we shall have
\[\dfrac{c}{a+b} = \dfrac{3}{2+4} = \frac{3}{6} = \frac{1}{2} = \frac{3}{2} - 3 + 6 - 12, \textrm{etc.}\]If \(a=10\), \(b=1\), and \(c=11\), we shall have
\[\dfrac{c}{a+b} = \dfrac{11}{10+1} = 1 = \frac{11}{10} - \frac{11}{100} + \frac{11}{1000} - \frac{11}{10000}, \textrm{etc.}\]Here if we consider only one term of the series, we have ¹¹⁄₁₀, which is too much by ⅒; if we take two terms, we have ⁹⁹⁄₁₀₀, which is too small by ¹⁄₁₀₀; ; if we take three terms, we have ¹⁰⁰¹⁄₁₀₀₀, which is too much by ¹⁄₁₀₀₀, etc.
304 When there are more than two terms in the divisor, we may also continue the division to infinity in the same manner. Thus, if the fraction \(\dfrac{1}{1-a+a^2}\) were proposed, the infinite scries, to which it is equal, will be found as follows:
We have therefore the equation
\[\dfrac{1}{1-a+a^2} = 1 + a -a^3 -a^4 + a^6 + a^7, \textrm{etc.};\]where, if we make \(a=1\), we have
1 = 1 + 1 - 1 - 1 + 1 + 1 - 1 - 1, etc.
which series contains twice the series found above 1 - 1 + 1 - 1, etc. Now, as we have found this to be ½, it is not extraordinary that we should find ²⁄₂, or 1, for the value of that which we have just determined.
By making \(a=\frac{1}{2}\), we shall have the equation
\[\dfrac{1}{\frac{3}{4}} = \frac{4}{3} = 1 + \frac{1}{2} - \frac{1}{8} - \frac{1}{16} + \frac{1}{64} + \frac{1}{128} - \frac{1}{512}, \textrm{etc.}\]If \(a=\frac{1}{3}\), we shall have the equation
\[\dfrac{1}{\frac{7}{9}} = \frac{9}{7} = 1 + \frac{1}{3} - \frac{1}{27} - \frac{1}{81} + \frac{1}{729}, \textrm{etc.}\]and if we take the four leading terms of this series, we have ¹⁰⁴⁄₈₁, which is only ¹⁄₅₆₇ less than ⁹⁄₇.
Suppose again \(a=\frac{2}{3}\), we shall have
\[\dfrac{1}{\frac{7}{9}} = \frac{9}{7} = 1 + \frac{2}{3} - \frac{8}{27} - \frac{16}{81} + \frac{64}{729}, \textrm{etc.}\]This series is therefore equal to the preceding one; and, by subtracting one from the other, we obtain ⅓ - ⁷⁄₂₇ - ¹⁵⁄₈₁ + ⁶³⁄₈₁, etc. which is necessarily = 0.
305 The method, which we have here explained, serves to resolve, generally, all fractions into infinite series; which is often found to be of the greatest utility. It is also remarkable, that an infinite series, though it never ceases, may have a determinate value. It should likewise be observed, that, from this branch of mathematics, inventions of the utmost importance have been derived; on which account the subject deserves to be studied with the greatest attention.
Editions
- Leonhard Euler. Elements of Algebra. Translated by Rev. John Hewlett. Third Edition. Longmans, Hurst, Rees, Orme, and Co. London. 1822.
- Leonhard Euler. Vollständige Anleitung zur Algebra. Mit den Zusätzen von Joseph Louis Lagrange. Herausgegeben von Heinrich Weber. B. G. Teubner. Leipzig and Berlin. 1911. Leonhardi Euleri Opera omnia. Series prima. Opera mathematica. Volumen primum.