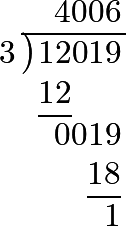Chapter 9. "Observations on the Rules of Proportion and their Utility."
Part I. Section III. Chapter 9. “Observations on the Rules of Proportion and their Utility.”
477 This theory is so useful in the common occurrences of life, that scarcely any person can do without it. There is always a proportion between prices and commodities; and when different kinds of money are the subject of exchange, the whole consists in determining their mutual relations. The examples furnished by these reflections will be very proper for illustrating the principles of proportion, and showing their utility by the application of them.
478 If we wished to know, for example, the relation between two kinds of money; suppose a Louis d’or and a ducat: we must first know the value of those pieces when compared with others of the same kind. Thus, a Louis d’or being, at Berlin, worth 5 Reichsthaler and 8 Groschen,1 and a ducat being worth 3 Reichsthaler, we may reduce these two values to one denomination; either to Reichsthaler, which gives the proportion
1 Louis : 1 ducat = 5⅓ Reichsthaler : 3 Reichsthaler = 16:9;
or to Groschen, in which case we have
1 Louis : 1 ducat = 128:72 = 16:9,
which proportions evidently give the true relation of the Louis d’or to the ducat; for the equality of the products of the extremes and the means gives, in both cases,
9 Louis d’or = 16 ducats;
and, by means of this comparison, we may change any sum of Louis d’or into ducats, and vice-versa. Thus, suppose it were required to find how many ducats there are in 1000 Louis d’or, we have this proportion:
9 Louis : 1000 Louis ∷ 16 ducats : 1777⁷⁄₉ ducats,
the number sought. If, on the contrary, it were required to find how many Louis d’or there are in 1000 ducats, we have the following proportion:
16 ducats : 1000 ducats ∷ 9 Louis : 562½ Louis,
the answer.
479 At St. Petersburg the value of the ducat varies, and depends on the course of exchange; which course determines the value of the ruble in Dutch stuivers, 105 of which make a ducat. So that when the exchange is at 45 stuivers per ruble, we have this proportion
1 ruble : 1 ducat = 45:105 = 3:7;
and hence this equality, 7 rubles = 3 ducats.
Hence again we shall find the value of a ducat in rubles; for
3 ducats : 7 rubles = 1 ducat : 2⅓ rubles;
that is, 1 ducat is equal to 2⅓ rubles.
But if the exchange were at 50 stuivers, the proportion would be,
1 ruble : 1 ducat = 50:105 = 10:21;
which would give 21 rubles = 10 ducats; whence 1 ducat = 2⅒ rubles. Lastly, when the exchange is at 44 stuivers, we have
1 ruble : 1 ducat = 44:105,
and thus2
1 ducat = 2¹⁷⁄₄₄ rubles = 2 rubles 38⁷⁄₁₁ kopeks.
480 It follows also from this, that we may compare different kinds of money, which we have frequently occasion to do in bills of exchange.
Suppose, for example, that a person of St. Petersburg has 1000 rubles to be paid to him at Berlin, and that he wishes to know the value of this sum in ducats at Berlin.
The exchange is at 47½; that is to say, one ruble makes 47½ stuivers; and in Holland, 20 stuivers make a Dutch guilder; 2½ guilders make a Dutch rijksdaalder: also, the exchange of Holland with Berlin is at 142; that is to say, for 100 Dutch rijksdaalder, 142 Reichsthaler are paid at Berlin; and lastly, the ducat is worth 3 Reichsthaler at Berlin.3
481 To resolve the question proposed, let us proceed step by step. Beginning therefore with the stuivers, since 1 ruble = 47½ stuivers, or 2 rubles = 95 stuivers, we shall have
2 rubles : 1000 rubles ∷ 95 stuivers : 47500 stuivers;
then again,
20 stuivers : 47500 stuivers ∷ 1 guilder : 2375 guilders
Also, since 2½ Dutch guilders = 1 Dutch rijksdaalder, or 5 Dutch guilders = 2 Dutch rijksdaalder; we shall have
5 guilders : 2375 guilders ∷ 2 rijksdaalder : 950 rijksdaalder.
Then, taking the Reichsthaler of Berlin, according to the exchange, at 142, we shall have
100 rijksdaalder : 950 rijksdaalder ∷ 142 Reichsthaler : 1349 Reichsthaler
And lastly,
3 Reichsthaler : 1349 Reichsthaler ∷ 1 ducat : 449⅔ ducats,
which is the number sought.
482 Now, in order to render these calculations still more complete, let us suppose that the Berlin banker refuses, under some pretext or other, to pay this sum, and to accept the bill of exchange without five per cent. discount; that is, paying only 100 instead of 105. In that case, we must make use of the following proportion:
105 : 100 ∷ 449⅔ : 428¹⁶⁄₆₃ ducats;
which is the answer under those conditions.
483 We have shown that six operations are necessary in making use of the Rule of Three; but we can greatly abridge those calculations by a rule which is called the Rule of Reduction, or Double Rule of Three. To explain which, we shall first consider the two antecedents of each of the six preceding operations:
| 1st | 2 rubles | : | 95 stuivers. |
| 2nd | 20 stuivers | : | 1 Dutch guilder |
| 3rd | 5 Dutch guilders | : | 2 Dutch rijksdaalder |
| 4th | 100 Dutch rijksdaalder | : | 142 Reichsthaler |
| 5th | 3 Reichsthaler | : | 1 ducat |
| 6th | 105 ducats | : | 100 ducats |
If we now look over the preceding calculations, we shall observe, that we have always multiplied the given sum by the third terms, or second antecedents, and divided the products by the first: it is evident, therefore, that we shall arrive at tlie same results bv multiplying at once the sum proposed by the product of all the third terms, and dividing by the product of all the first terms: or, which amounts to the same thing, that we have only to make the following proportion: As the product of all the first terms, is to the given number of rubles, so is the product of all the second terms, to the number of ducats payable at Berlin.
484 This calculation is abridged still more, when amongst the first terms some are found that have common divisors with the second or third terms; for, in this case, we destroy those terms, and substitute the quotient arising from the division by that common divisor. The preceding example will, in this manner, assume the following form.
\[(2\cdot 20\cdot 5\cdot 100\cdot 3\cdot 105) : 1000 :: (95\cdot 2\cdot 142\cdot 100) : \dfrac{1000\cdot 95\cdot 2\cdot 142\cdot 100}{2\cdot 20\cdot 5\cdot 100\cdot 3\cdot 105};\]and after cancelling the common divisors in the numerator and denominator, this will become
\[\dfrac{10\cdot 19\cdot 142}{3\cdot 21} = \frac{26980}{63} = 428\frac{16}{63} \, \textrm{ducats},\]as before.
485 The method which must be observed in using the Rule of Reduction is this: we begin with the kind of money in question, and compare it with another which is to begin the next relation, in which we compare this second kind with a third, and so on. Each relation, therefore, begins with the same kind as the preceding relation ended with; and the operation is continued till we arrive at the kind of money which the answer requires; at the end of which we must reckon the fractional remainders.
486 Let us give some other examples, in order to facilitate the practice of this calculation.
If ducats gain at Hamburg 1 per cent., on 2 Reichsthaler Banco (that is to say, if 50 ducats are worth, not 100, but 101 Reichsthaler Banco), and if the exchange between Hamburg and Konigsberg is 119 Polish grosz (that is, if 1 Reichsthaler Banco is equal to 119 Polish grosz), how many Polish złoty are equivalent to 1000 ducats (it being understood that 30 Polish grosz make 1 Polish złoty)?
- 50 ducats = 101 Reichsthaler Banco
- 1 Reichsthaler Banco = 119 grosz
- 30 grosz = 1 złoty
Therefore 1500 ducats = 12019 złoty.
hence 500 ducats = 4006⅓ złoty. Therefore, 1000 ducats = 8012⅔ złoty
487 We will propose another example, which may still farther illustrate this method.
Ducats of Amsterdam are brought to Leipzig, having in the former city the value of 5 guilders 4 stuivers current (that is to say, 1 ducat is worth 104 Dutch stuivers, and 5 ducats are worth 26 Dutch guilders). If, therefore, the agio of the bank at Amsterdam is 5 per cent. (that is, if 105 current are equal to 100 banco),4 and if the exchange from Leipzig to Amsterdam, in bank money, is 133¼ per cent. (that is, if for 100 Dutch rijksdaalder banco we pay at Leipzig 133¼ Thaler current); and lastly, 2 Dutch rijksdaalder making 5 Dutch guilder; it is required to determine how many Thaler we must pay at Leipzig, according to these exchanges, for 1000 ducats?
- 5 ducats = 26 guilders current
- 105 guilders current = 100 guilders banco; so 21 guilders current = 20 guilders banco
- 5 guilder banco = 2 rijksdaalder banco
- 100 rijksdaalder banco = 133¼ Thaler current in Leipzig; so 400 rijksdaalder banco = 533 Thaler current in Leipzig
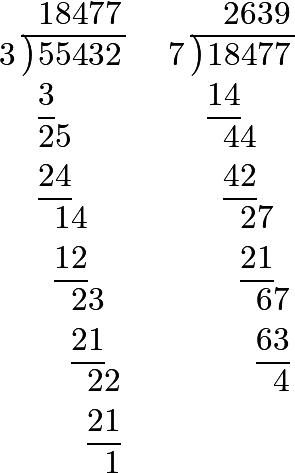
Therefore 210000 ducats = 554320 Thaler in Leipzig; so 21000 ducats = 55432 Thaler in Leipzig.
Thus dividing by 3,
7000 ducats = 18477⅓ Thaler in Leipzig;
and dividing by 7,
1000 ducats = 2639⁴⁄₇ + ¹⁄₂₁ Thaler in Leipzig = 2639¹³⁄₂₁ Thaler in Leipzig.
Editions
- Leonhard Euler. Elements of Algebra. Translated by Rev. John Hewlett. Third Edition. Longmans, Hurst, Rees, Orme, and Co. London. 1822.
- Leonhard Euler. Vollständige Anleitung zur Algebra. Mit den Zusätzen von Joseph Louis Lagrange. Herausgegeben von Heinrich Weber. B. G. Teubner. Leipzig and Berlin. 1911. Leonhardi Euleri Opera omnia. Series prima. Opera mathematica. Volumen primum.
-
1 Reichsthaler = 24 Groschen. ↩
-
1 ruble = 100 kopeks. ↩
-
1 Dutch rijksdaalder = 2½ Dutch guilders. ↩
-
Wiktionary: “agio”: “The premium or percentage on a better sort of money when it is given in exchange for an inferior sort.” ↩