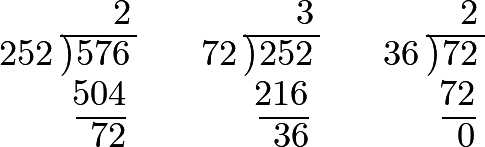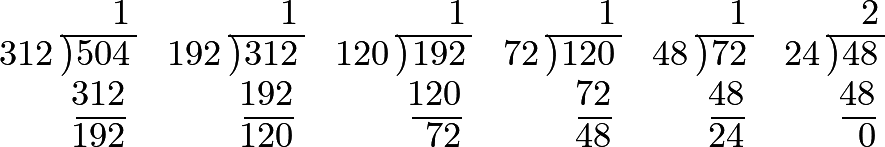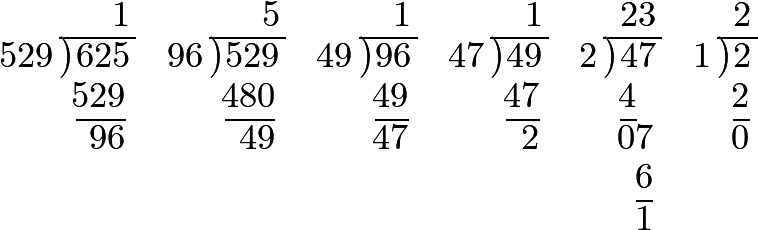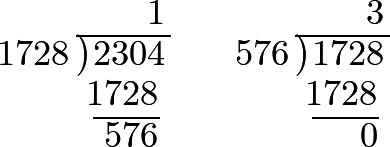Chapter 7. "Of the Greatest Common Divisor of two given Numbers."
Part I. Section III. Chapter 7. “Of the Greatest Common Divisor of two given Numbers.”
451 There are some numbers which have no other common divisor than unity; and when the numerator and denominator of a fraction are of this nature, it cannot be reduced to a more convenient form. The two numbers 48 and 35, for example, have no common divisor, though each has its own divisors; for which reason, we cannot express the relation 48:35 more simply, because the division of two numbers by 1 does not diminish them.
452 But when the two numbers have a common divisor, it is found, and even the greatest which they have, by the following Rule:
Divide the greater of the two numbers by the less; next, divide the preceding divisor by the remainder; what remains in this second division will afterwards become a divisor for a third division, in which the remainder of the preceding divisor will be the dividend. We must continue this operation till we arrive at a division that leaves no remainder; and this last divisor will be the greatest common divisor of the two given numbers.
Thus, for the two numbers 576 and 252.
So that, in this instance, the greatest common divisor is 36.
453 It will be proper to illustrate this rule by some other examples; and, for this purpose, let the greatest common divisor of the numbers 504 and 312 be required.
So that 24 is the greatest common divisor, and consequently the relation 504:312 is reduced to the form 21:13.
454 Let the relation 625:529 be given, and the greatest common divisor of these two numbers be required.
Wherefore 1 is, in this case, the greatest common divisor, and consequently we cannot express the relation 625:529 by less numbers, nor reduce it to simpler terms.
455 It may be necessary, in this place, to give a demonstration of the foregoing Rule. In order to this, let \(a\) be the greater, and \(b\) the less of the given numbers; and let \(d\) be one of their common divisors; it is evident that \(a\) and \(b\) being divisible by \(d\), we may also divide the quantities, \(a - b\), \(a - 2b\), \(a - 3b\), and, in general, \(a - nb\) by \(d\).
456 The converse is no less true: that is, if the numbers \(b\) and \(a - nb\) are divisible by \(d\), the number \(a\) will also be divisible by \(d\); for \(nb\) being divisible by \(n\), we could not divide \(a - nb\) by \(d\), if \(a\) were not also divisible by \(d\).
457 We observe farther, that if \(d\) be the greatest common divisor of two numbers, \(b\) and \(a - nb\), it will also be the greatest common divisor of the two numbers \(a\) and \(b\); for if a greater common divisor than \(d\) could be found for these numbers \(a\) and \(b\), that number would also be a common divisor of \(b\) and \(a - nb\); and consequently \(d\) would not be the greatest common divisor of these two numbers: but we have supposed \(d\) the greatest divisor common to \(b\) and \(a - nb\); therefore \(d\) must also be the greatest common divisor of \(a\) and \(b\).
458 These things being laid down, let us divide, according to the rule, the greater number \(a\) by the less \(b\); and let us suppose the quotient to be \(n\); then the remainder will be \(a - nb\), which must necessarily be less than \(b\); and this remainder \(a - nb\) having the same greatest common divisor with \(b\), as the given numbers \(a\) and \(b\), we have only to repeat the division, dividing the preceding divisor \(b\) by the remainder \(a - nb\); and the new remainder which we obtain will still have, with the preceding divisor, the same greatest common divisor, and so on.
459 We proceed, in the same manner, till we arrive at a is nothing. Let therefore \(p\) be the last divisor, contained exactly a certain number of times in its dividend; this dividend will evidently be divisible by \(p\), and will have the form \(mp\); so that the numbers \(p\) and \(mp\) are both divisible by \(p\): and it is also evident that they have no greater common divisor, because no number can actually be divided by a number greater than itself; consequently, this last divisor is also the greatest common divisor of the given numbers \(a\) and \(b\).
460 We will now give another example of the same rule, requiring the greatest common divisor of the numbers 1728 and 2304. The operation is as follows:
Hence it follows that 576 is the greatest common divisor, and that the relation 1728:2304 is reduced to 3:4; that is to say, 1728 is to 2304 in the same relation as 3 is to 4.
Editions
- Leonhard Euler. Elements of Algebra. Translated by Rev. John Hewlett. Third Edition. Longmans, Hurst, Rees, Orme, and Co. London. 1822.
- Leonhard Euler. Vollständige Anleitung zur Algebra. Mit den Zusätzen von Joseph Louis Lagrange. Herausgegeben von Heinrich Weber. B. G. Teubner. Leipzig and Berlin. 1911. Leonhardi Euleri Opera omnia. Series prima. Opera mathematica. Volumen primum.