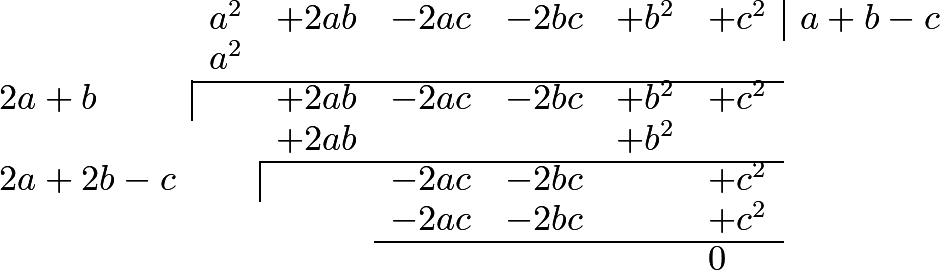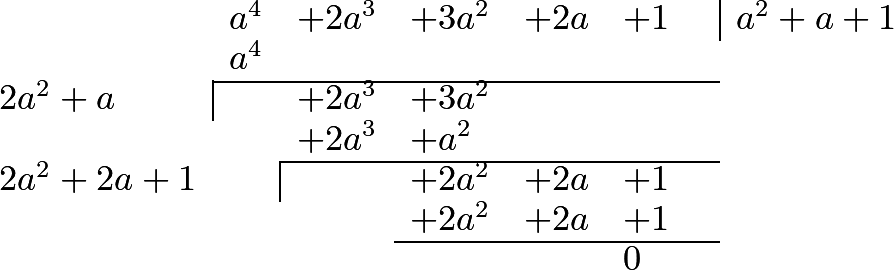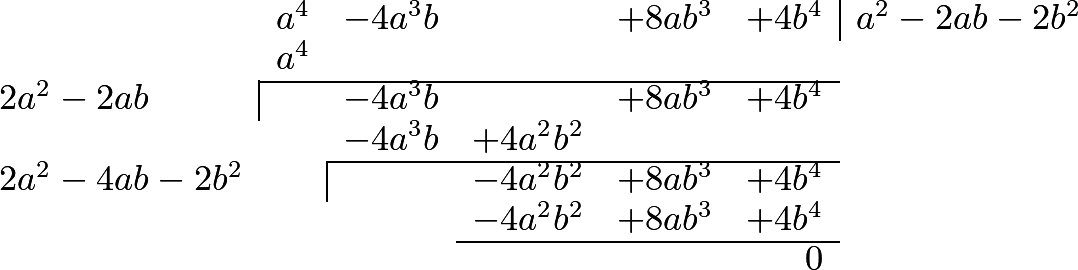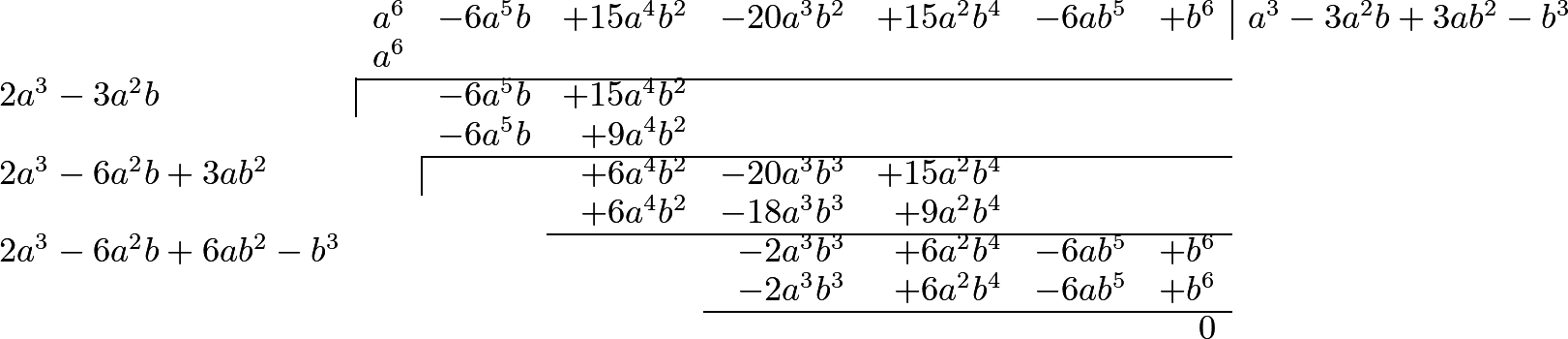Chapter 7. "Of the Extraction of Roots applied to Compound Quantities."
Part I. Section II. Chapter 7. “Of the Extraction of Roots applied to Compound Quantities.”
317 In order to give a certain rule for this operation, we must consider attentively the square of the root \(a+b\), which is \(a^2+2ab+b^2\), in order that we may reciprocally find the root of a given square.
318 We must consider therefore, first, that as the square, \(a^2+2ab+b^2\), is composed of several terms, it is certain that the root also will comprise more than one term; and that if we write the terms of the square in such a manner, that the powers of one of the letters, as \(a\), may go on continually diminishing, the first term will be the square of the first term of the root; and since, in the present case, the first term of the square is \(a^2\), it is certain that the first term of the root is \(a\).
319 Having therefore found the first term of the root, that is to say, \(a\), we must consider the rest of the square, namely, \(2ab+b^2\), to see if we can derive from it the second part of the root, which is \(b\). Now, this remainder, \(2ab+b^2\), may be represented by the product, \((2a+b)b\); wherefore the remainder having two factors, \((2a+b)\), and \(b\), it is evident that we shall find the latter, \(b\), which is the second part of the root, by dividing the remainder, \(2ab+b^2\), by \(2a+b\).
320 So that the quotient, arising from the division of the above remainder by \(2a+b\), is the second term of the root required; and in this division we observe, that \(2a\) is the double of the first term \(a\), which is already determined: so that although the second term is yet unknown, and it is necessary, for the present, to leave its place empty, we may nevertheless attempt the division, since in it we attend only to the first term \(2a\); but as soon as the quotient is found, which in the present case is \(b\), we must put it in the vacant place, and thus render the division complete.
321 The calculation, therefore, by which we find the root of the square \(a^2+2ab+b^2\), may be represented thus
\[\begin{array}{rrrrrrr} &&a^2&+2ab&+b^2&\vert&a+b\\ &&a^2&&&&\\ \hline 2a+b&\vert&&2ab&+b^2&\\ &&&2ab&+b^2&\\ \hline &&&&0.&& \end{array}\]322 We may, also, in the same manner, find the square root of other compound quantities, provided they are squares, as will appear from the following examples:
\[\begin{array}{rrrrrrr} &&a^2&+6ab&+9b^2&\vert&a+3b\\ &&a^2&&&&\\ \hline 2a+3b&\vert&&6ab&+9b^2&\\ &&&6ab&+9b^2&\\ \hline &&&&0.&& \end{array}\]\[\begin{array}{rrrrrrr} &&4a^2&-4ab&+b^2&\vert&2a-b\\ &&4a^2&&&&\\ \hline 4a-b&\vert&&-4ab&+b^2&\\ &&&-4ab&+b^2&\\ \hline &&&&0.&& \end{array}\]
\[\begin{array}{rrrrrrr} &&9p^2&+24pq&+16q^2&\vert&3p+4q\\ &&9p^2&&&&\\ \hline 6p+4q&\vert&&24pq&+16q^2&\\ &&&24pq&+16q^2&\\ \hline &&&&0.&& \end{array}\]
\[\begin{array}{rrrrrrr} &&25x^2&-60x&+36&\vert&5x-6\\ &&25x^2&&&&\\ \hline 10x-6&\vert&&-60x&+36&\\ &&&-60x&+36&\\ \hline &&&&0.&& \end{array}\]
323 When there is a remainder after the division, it is a proof that the root is composed of more than two terms. We must in that case consider the two terms already found as forming the first part, and endeavour to derive the other from the remainder, in the same manner as we found the second term of the root from the first. The following examples will render this operation more clear.
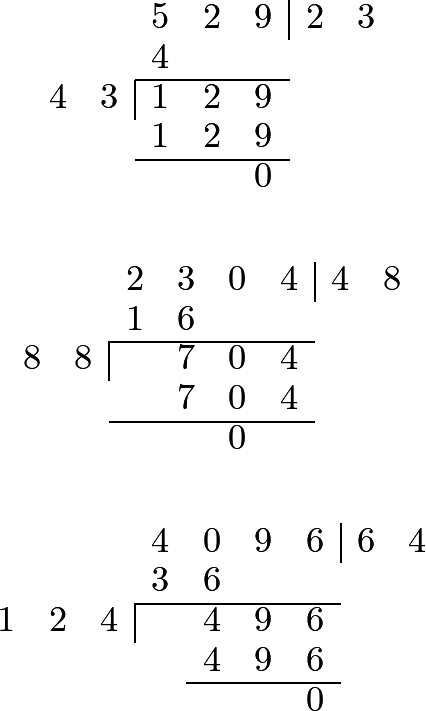
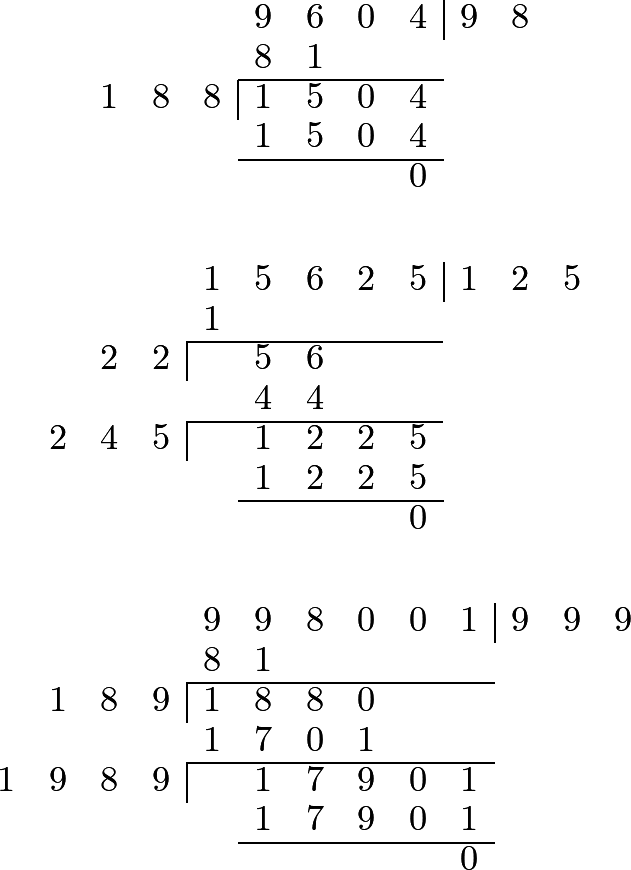
324 We easily deduce from the rule which we have explained, the method which is taught in books of arithmetic for the extraction of the square root, as will appear from the following examples in numbers:1 2 3 4




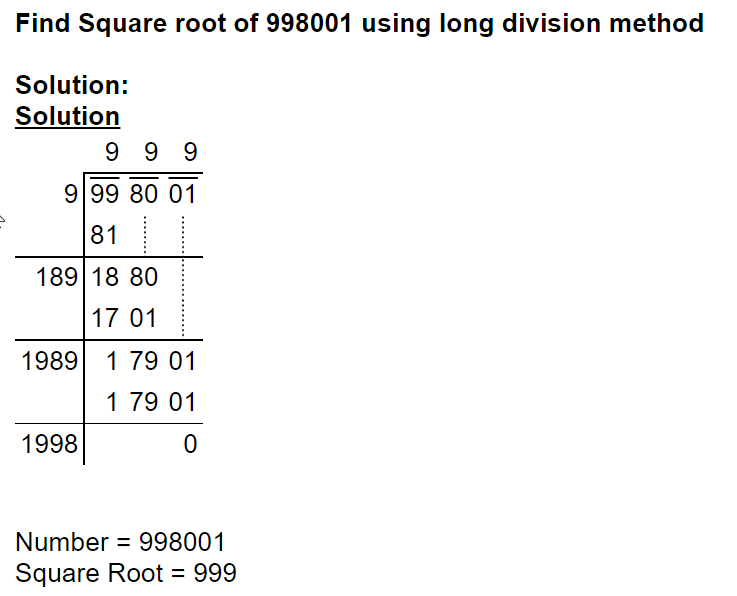
325 But when there is a remainder after all the figures have been used, it is a proof that the number proposed is not a square; and, consequently, that its root cannot be assigned. In such cases, the radical sign, which we before employed, is made use of. This is written before the quantity, and the quantity itself is placed between parentheses, or under a line: thus, the square root of \(a^2+b^2\) is represented by \(\surd(a^2+b^2)\), or by \(\sqrt{a^2+b^2}\); and \(\surd(1-x^2)\), or \(\sqrt{1-x^2}\), expresses the square root of \(1-x^2\). Instead of this radical sign, we may use the fractional exponent \(\frac{1}{2}\), and represent the square root of \(a^2+b^2\), for instance, by \((a^2+b^2)^{\frac{1}{2}}\).
Editions
- Leonhard Euler. Elements of Algebra. Translated by Rev. John Hewlett. Third Edition. Longmans, Hurst, Rees, Orme, and Co. London. 1822.
- Leonhard Euler. Vollständige Anleitung zur Algebra. Mit den Zusätzen von Joseph Louis Lagrange. Herausgegeben von Heinrich Weber. B. G. Teubner. Leipzig and Berlin. 1911. Leonhardi Euleri Opera omnia. Series prima. Opera mathematica. Volumen primum.
-
AtoZmath.com: Pre-Algebra Calculators. 12.2 Radicals. 7. Square root by long division method. ↩
-
Paul E. Black, “square root”, in Dictionary of Algorithms and Data Structures [online], Paul E. Black, ed. 6 May 2019. Available from: https://www.nist.gov/dads/HTML/squareRoot.html ↩
-
CK-12: CK-12 CBSE Maths Class 8. Last Modified: Apr 28, 2021. 6.2 Square Roots - Definition, Properties, Methods and Examples ↩
-
AlgebraDen.com: Square Root by Long Division Method ↩