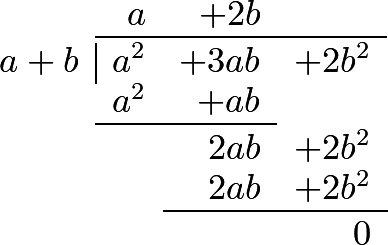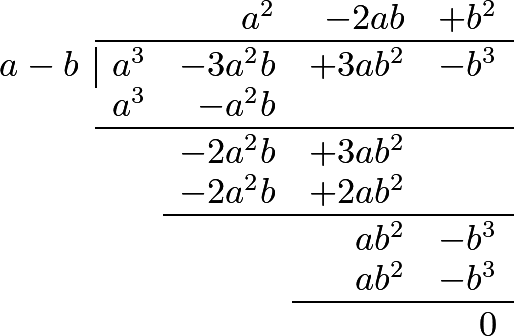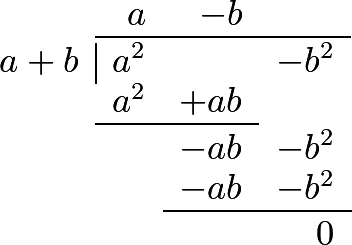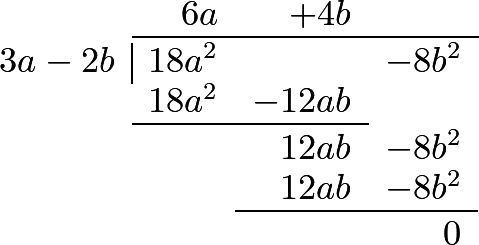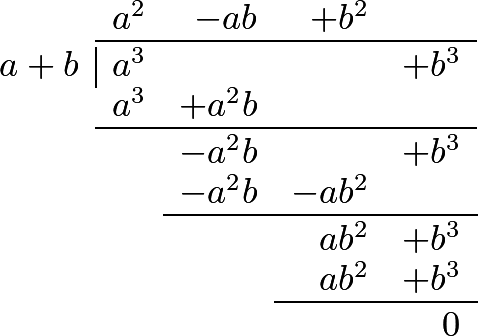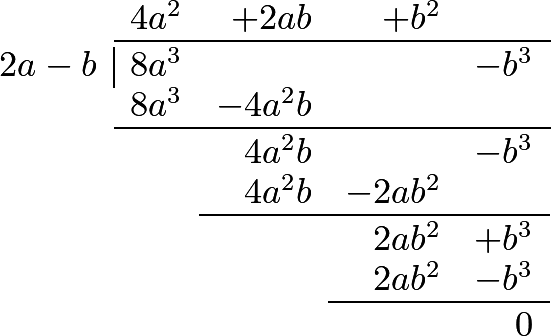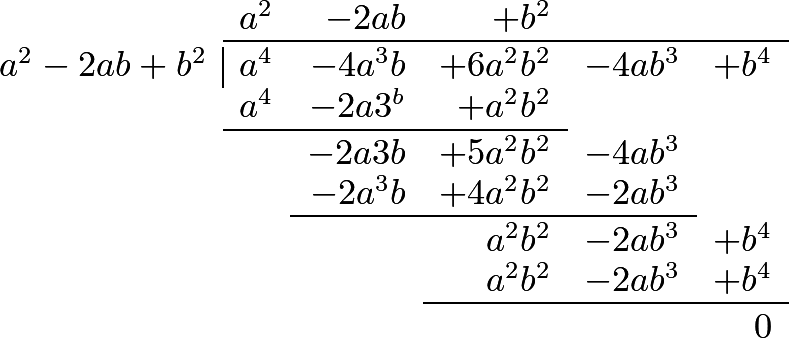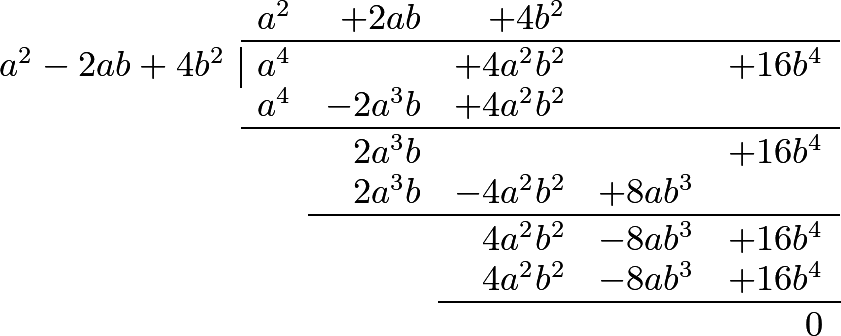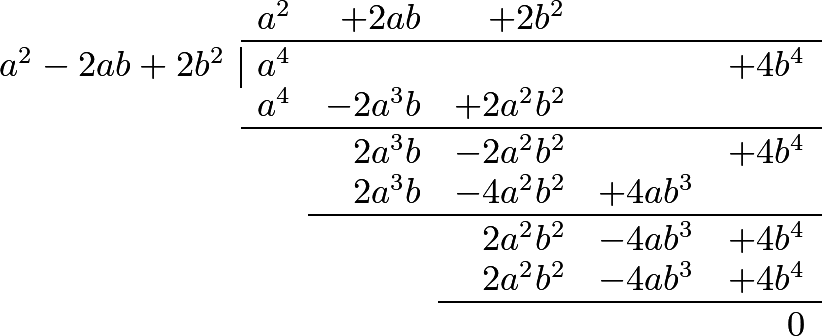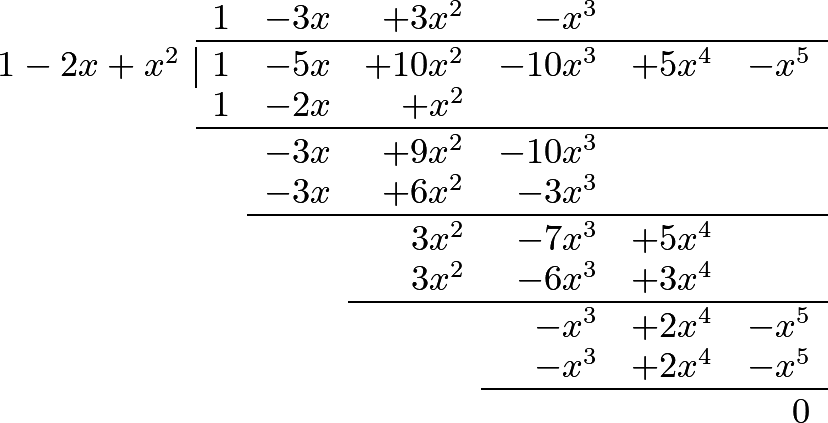Chapter 4. "Of the Division of Compound Quantities."
Part I. Section II. Chapter 4. “Of the Division of Compound Quantities.”
282 When we wish simply to represent division, we make use of the usual mark of fractions; which is, to write the denominator under the numerator, separating them by a line; or to enclose each quantity between parentheses, placing two points between the divisor and dividend, and a line between them. Thus, if it were required, for example, to divide \(a + b\) by \(c + d\), we should represent the quotient thus; \(\frac{a+b}{c+d}\), according to the former method; and thus, \((a + b):(c + d)\) according to the latter, where each expression is read \(a + b\) divided by \(c + d\).
283 When it is required to divide a compound quantity by a simple one, we divide each term separately, as in the following examples:
\[\begin{gather} (6a-8b+4c):(2) = 3a-4b+2c\\ (a^2-2ab):(a) = a-2b\\ (a^3-2aab+3abb):(a) = aa-2ab+3bb\\ (4aa-6aac+8abc):(2a) = 2ab-3ac+4bc\\ (9aabc-12abbc+15abcc):(3abc) = 3a-4b+5c, \textrm{etc.} \end{gather}\]284 If it should happen that a term of the dividend is not divisible by the divisor, the quotient is represented by a fraction, as in the division of \(a+b\) by \(a\), which gives \(1+\frac{b}{a}\). Likewise,
\[(aa-ab+bb):(aa) = 1-\frac{b}{a}+\frac{bb}{aa}.\]In the same manner, if we divide \(2a+b\) by 2, we obtain \(a+\frac{b}{2}\): and here it may be remarked, that we may write \(\frac{1}{2}b\), instead of \(\frac{b}{2}\), because \(\frac{1}{2}\) times \(b\) is equal to \(\frac{b}{2}\); and, in the same manner, \(\frac{b}{3}\) is the same as \(\frac{1}{3}b\), and \(\frac{2b}{3}\) the same as \(\frac{2}{3}b\), etc.
285 But when the divisor is itself a compound quantity, division becomes more difficult. This frequently occurs where we least expect it; and when it cannot be performed, we must content ourselves with representing the quotient by a fraction, in the manner that we have already described. At present, we will begin by considering some cases in which actual division takes place.
286 Suppose, for example, it were required to divide \(ac-bc\) by \(a-b\), the quotient must here be such as, when multiplied by the divisor \(a - b\), will produce the dividend \(ac - bc\). Now, it is evident, that this quotient must include \(c\), since without it we could not obtain \(ac\); in order therefore to try whether \(c\) is the whole quotient, we have only to multiply it by the divisor, and see if that multiplication produces the whole dividend, or only a part of it. In the present case, if we multiply \(a - b\) by \(c\), we have \(ac - bc\), which is exactly the dividend; so that \(c\) is the whole quotient. It is no less evident, that
\[\begin{gather} (aa+ab):(a+b)=a\\ (3aa-2ab):(3a-2b)=a\\ (6aa-9ab):(2a-3b)=3a, \textrm{etc.} \end{gather}\]287 We cannot fail, in this way, to find a part of the quotient; if, therefore, what we have found, when multiplied by the divisor, does not exhaust the dividend, we have only to divide the remainder again by the divisor, in order to obtain a second part of the quotient; and to continue the same method, until we have found the whole.
Let us, as an example, divide \(a^2+3ab+2b^2\) by \(a+b\). It is evident, in the first place, that the quotient will include the term a, since otherwise we should not obtain aa. Now, from the multiplication of the divisor \(a+b\) by \(a\), arises \(aa+ab\); which quantity being subtracted from the dividend, leaves the remainder, \(2ab+2b^2\); and this remainder must also be divided by \(a+b\), where it is evident that the quotient of this division must contain the term \(2b\). Now, \(2b\), multiplied by \(a + b\), produces \(2ab+2b^2\); consequently, \(a + 2b\) is the quotient required; which multiplied by the divisor a + b, ought to produce the dividend \(a^2+3ab+2b^2\). See the operation.1
288 This operation will be considerably facilitated by choosing one of the terms of the divisor, which contains the highest power, to be written first, and then, in arranging the terms of the dividend, begin with the highest powers of that first term of the divisor, continuing it according to the powers of that letter. This term in the preceding example was \(a\). The following examples will render the process more perspicuous.
Editions
- Leonhard Euler. Elements of Algebra. Translated by Rev. John Hewlett. Third Edition. Longmans, Hurst, Rees, Orme, and Co. London. 1822.
- Leonhard Euler. Vollständige Anleitung zur Algebra. Mit den Zusätzen von Joseph Louis Lagrange. Herausgegeben von Heinrich Weber. B. G. Teubner. Leipzig and Berlin. 1911. Leonhardi Euleri Opera omnia. Series prima. Opera mathematica. Volumen primum.
-
Made using Tables Generator and TeXeR ↩