The $C^{\mathrm{\infty }}$ Urysohn lemma

Define $\eta :ℝ\to ℝ$ by

$$\eta (t)=e^{-1/t}{1}_{(0,\mathrm{\infty })}(t).$$

It is a fact that $\eta$ is $C^{\mathrm{\infty }}$. This is proved by showing that for each $k\ge 1$ there is a polynomial $P_k$ of degree $2k$ such that ${\eta }^{(k)}(t)=P_k(t^{-1})e^{-1/t}$ for $t>0$, and that ${\eta }^{(k)}(0)=0$, which together imply that $\eta \in C^k$.

Define $\psi :{ℝ}^d\to ℝ$ by

Because $x\mapsto 1-{|x|}^2$ is $C^{\mathrm{\infty }}:{ℝ}^d\to ℝ$, the chain rule tells us that $\psi$ is $C^{\mathrm{\infty }}$.

For a function $\varphi$ on ${ℝ}^d$ and for $t>0$, we define

$${\varphi }_t(x)=t^{-d}\varphi (t^{-1}x).$$

We now construct bump functions.

Theorem 1 ($C^{\mathrm{\infty }}$ Urysohn lemma).

If $K$ is a compact subset of ${\mathrm{R}}^d$ and $U$ is an open set containing $K$, then there exists $\varphi \mathrm{\in }{C}^{\mathrm{\infty }}\mathit{}\mathrm{(}{\mathrm{R}}^d\mathrm{)}$ with $\mathrm{0}\mathrm{\le }\varphi \mathrm{\le }\mathrm{1}$, $\varphi \mathrm{=}\mathrm{1}$ on $K$, and $\mathrm{supp}\mathit{}\varphi \mathrm{\subset }U$. Moreover, if $K$ is invariant under $S\mathit{}O\mathit{}\mathrm{(}d\mathrm{)}$ then the function $\varphi$ constructed here is radial.

Proof.

Let

$$\delta =d(K,U^c),$$

which is positive because $K$ is compact and $U^c$ is closed. Let

and define $f$ on ${ℝ}^d$ by

$$f={\left({\int }_{{ℝ}^d}\psi (x)𝑑x\right)}^{-1}{\psi }_{\delta /3},$$

whose support is

$$\mathrm{supp}f=\mathrm{supp}{\psi }_{\delta /3}=\overline{B_{\delta /3}}.$$

Finally define $\varphi$ on ${ℝ}^d$ by

$$\varphi =1_V*f.$$

Because $V$ is bounded and $f$ is $C^{\mathrm{\infty }}$, the function $\varphi$ is $C^{\mathrm{\infty }}$. The support of $\varphi$ is

$$\mathrm{supp}\varphi =\mathrm{supp}(1_V*f)\subset \overline{\mathrm{supp}{\mathrm{\hspace{0.17em}1}}_V+\mathrm{supp}f}=\overline{V+\overline{B_{\delta /3}}}=K+\overline{B_{2\delta /3}}\subset U.$$

Because $1_V$ and $f$ are nonnegative, so is their convolution $\varphi$. For any $x$,

$$\varphi (x)={\int }_{{ℝ}^d}{1}_V(x-y)f(y)𝑑y\le {\int }_{{ℝ}^d}f(y)𝑑y=1,$$

so $0\le \varphi \le 1$. For $x\in K$, if $y\in V^c$ then $|x-y|\ge \delta /3$. But $f(u)=0$ for $|u|\ge \delta /3$, so in this case $f(x-y)=0$. This implies that for $x\in K$ the functions $y\mapsto 1_V(y)f(x-y)$ and $y\mapsto f(x-y)$ are equal, hence

$$\varphi (x)={\int }_{{ℝ}^d}{1}_V(y)f(x-y)𝑑y={\int }_{{ℝ}^d}f(x-y)𝑑y={\int }_{{ℝ}^d}f(y)𝑑y=1.$$

This shows that $\varphi =1$ on $K$, verifying all the assertions made about $\varphi$.

The function $\psi$ is radial and so $f$ is too. If $V$ is invariant under $SO(d)$, then the indicator function $1_V$ is radial. Thus, if $K$ is invariant under $SO(d)$ then $1_V$ is radial, and the convolution of two radial functions is also radial, which means that $\varphi$ is radial in this case. ∎

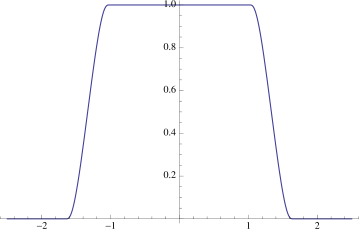
For example, take $d=1$, take $K$ to be the closed ball of radius $1$, and take $U$ to be the open ball of radius $2$. Then $\delta =d(K,U^c)=1$ and $V=B_{4/3}$. In Figure 1 we plot the bump function $\varphi$ constructed in the above theorem.

Figure 1: The bump function $\varphi$, for $d=1$, $K=[-1,1]$, $U=(-2,2)$; $\delta =1$ and $V=(-4/3,4/3)$